Назад | Содержание | Вперёд
Существует несколько аспектов эффективности программ, включая такие наиболее общие, как время выполнения и требования по объему памяти. Другим аспектом является время, необходимое программисту для разработки программы.
Традиционная архитектура вычислительных машин не очень хорошо приспособлена для реализации прологовского способа выполнения программ, предусматривающего достижение целей из некоторого списка. Поэтому ограниченность ресурсов по времени и пространству сказывается в Прологе, пожалуй, в большей степени, чем в большинстве других языков программирования. Вызовет ли это трудности в практических приложениях, зависит от задачи. Фактор времени практически не имеет значения, если пролог-программа, которую запускают по несколько раз в день, занимает 1 секунду процессорного времени, а соответствующая программа на каком-либо другом языке, скажем на Фортране, - 0.1 секунды. Разница в эффективности становится существенной, если эти две программы требуют 50 и 5 минут соответственно.
С другой стороны, во многих областях применения Пролога он может существенно сократить время разработки программ. Программы на Прологе, вообще говоря, легче писать, легче понимать и отлаживать, чем программы, написанные на традиционных языках. Задачи, тяготеющие к "царству Пролога", включают в себя обработку символьной, нечисловой информации, структурированных объектов данных и отношений между ними. Пролог успешно применяется, в частности. в таких областях, как символьное решение уравнений, планирование, базы данных, автоматическое решение задач, машинное макетирование, реализация языков программирования, дискретное и аналоговое моделирование, архитектурное проектирование, машинное обучение, понимание естественного языка, экспертные системы и другие задачи искусственного интеллекта. С другой стороны, применение Пролога в области вычислительной математики вряд ли можно считать
естественным.Если программа страдает неэффективностью, то ее обычно можно кардинально улучшить, изменив сам алгоритм. Однако для того, чтобы это сделать, необходимо изучить процедурные аспекты программы. Простой способ сокращения времени выполнения состоит в нахождении более удачного порядка предложений в процедуре и целей - в телах процедур. Другой, относительно простой метод заключается в управлении действиями системы посредством отсечений.
Полезные идеи, относящиеся к повышению эффективности, обычно возникают только при достижении более глубокого понимания задачи. Более эффективный алгоритм может, вообще говоря, привести к улучшениям двух видов:
Мы изучим оба вида улучшений на примерах. Кроме того, мы рассмотрим на примере еще один метод повышения эффективности. Этот метод основан на добавлении в базу данных тех промежуточных результатов, которые с большой вероятностью могут потребоваться для дальнейших вычислений. Вместо того, чтобы вычислять их снова, программа просто отыщет их в базе данных как уже известные факты.
В качестве простого примера повышения эффективности давайте вернемся к задаче о восьми ферзях (см. рис. 4.7). В этой программе Y-координаты ферзей перебираются последовательно - для каждого ферзя пробуются числа от 1 до 8. Этот процесс был запрограммирован в виде цели
принадлежит( Y, [1, 2, 3, 4, 5, 6, 7, 8] )
Процедура принадлежит работает так: вначале пробует Y = 1, затем Y = 2, Y = 3 и т.д. Поскольку ферзи расположены один за другим в смежных вертикалях доски, очевидно, что такой порядок перебора не является оптимальным. Дело в том, что ферзи, расположенные в смежных вертикалях будут бить друг друга, если они не будут разнесены по вертикали на расстояние, превышающее, по крайней мере одно поле. В соответствии с этим наблюдением можно попытаться повысить эффективность, просто изменив порядок рассмотрения координат-кандидатов. Например:
принадлежит( Y, [1, 5, 2, 6, 3, 7, 4, 8] )
Это маленькое изменение уменьшит время, необходимое для нахождения первого решения, в 3-4 раза.
В следующем примере такая же простая идея, связанная с изменением порядка, превращает практически неприемлемую временную сложность в тривиальную.
Задача раскраски карты состоит в приписывании каждой стране на заданной карте одного из четырех заданных цветов с таким расчетом, чтобы ни одна пара соседних стран не была окрашена в одинаковый цвет. Существует теорема, которая гарантирует, что это всегда возможно.
Пусть карта задана отношением соседства
соседи( Страна, Соседи)
где Соседи - список стран, граничащих со страной Страна. При помощи этого отношения карта Европы с 20-ю странами будет представлена (в алфавитном порядке) так:
соседи( австрия,
[венгрия, запгермания, италия,
лихтенштейн, чехословакия,
швейцария, югославия]),
соседи( албания, [греция, югославия]).
соседи( андорра, [испания, франция]).
. . .
Решение представим в виде списка пар вида
Страна / Цвет
которые устанавливают цвет для каждой страны на данной карте. Для каждой карты названия стран всегда известны заранее, так что задача состоит в нахождении цветов. Таким образом, для Европы задача сводится к отысканию подходящей конкретизации переменных C1, C2, СЗ и т.д. в списке
[австрия/C1, албания/С2, андорра/С3, . . .]
Теперь определим предикат
цвета( СписЦветСтран)
который истинен, если СписЦветСтран удовлетворяет тем ограничениям, которые наложены на раскраску отношением соседи. Пусть четырьмя цветами будут желтый, синий, красный и зеленый. Условие запрета раскраски соседних стран в одинаковый цвет можно сформулировать на Прологе так:
цвета( [ ]).
цвета( [Страна/Цвет |
Остальные] ) :-
цвета( Остальные),
принадлежит(
Цвет, [желтый, синий, красный, зеленый]),
not(
принадлежит( Страна1/Цвет, Остальные),
сосед( Страна, Страна1) ).
сосед( Страна,
Страна1) :-
соседи( Страна, Соседи),
принадлежит( Страна1, Соседи).
Здесь принадлежит( X, L) - как всегда, отношение принадлежности к списку. Для простых карт с небольшим числом стран такая программа будет работать. Что же касается Европы, то здесь результат проблематичен. Если считать, что мы располагаем встроенным предикатом setof, то можно попытаться раскрасить карту Европы следующим образом. Определим сначала вспомогательное отношение:
страна( С) :- соседи( С, _ ).
Тогда вопрос для раскраски карты Европы можно сформулировать так:
?- sеtоf( Стр/Цвет,
страна( Стр), СписЦветСтран),
цвета(
СписЦветСтран).
Цель setof - построить "шаблон" списка СписЦветСтран, в котором в элементах вида страна/ цвет вместо цветов будут стоять неконкретизированные переменные. Предполагается, что после этого цель цвета конкретизирует их. Такая попытка скорее всего потерпит неудачу вследствие неэффективности работы программы.
Тщательное исследование способа, при помощи которого пролог-система пытается достичь цели цвета, обнаруживает источник неэффективности. Страны расположены в списке в алфавитном порядке, а он не имеет никакого отношения к их географическим связям. Порядок, в котором странам приписываются цвета, соответствует порядку их расположения в списке (с конца к началу), что в нашем случае никак не связано с отношением соседи. Поэтому процесс раскраски начинается в одном конце карты, продолжается в другой и т.д., перемещаясь по ней более или менее случайно. Это легко может привести к ситуации, когда при попытке раскрасить очередную страну окажется, что она окружена странами, уже раскрашенными во все четыре доступных цвета. Подобные ситуации приводят к возвратам, снижающим эффективность.
Ясно поэтому, что эффективность зависит от порядка раскраски стран. Интуиция подсказывает простую стратегию раскраски, которая должна быть лучше, чем случайная: начать со страны, имеющей иного соседей, затем перейти к ее соседям, затем - к соседям соседей и т.д. В случае Европы хорошим кандидатом для начальной страны является Западная Германия (как имеющая наибольшее количество соседей - 9). Понятно, что при построении шаблона списка элементов вида страна/цвет Западную Германию следует поместить в конец этого списка, а остальные страны - добавлять со стороны его начала. Таким образом, алгоритм раскраски, который начинает работу с конца списка, в начале займется Западной Германией и продолжит работу, переходя от соседа к соседу.
Новый способ упорядочивания списка стран резко повышает эффективность по отношению к исходному, алфавитному порядку, и теперь возможные раскраски карты Европы будут получены без труда.
Можно было бы построить такой правильно упорядоченный список стран вручную, но в этом нет необходимости. Эту работу выполнит процедура создспис. Она начинает построение с некоторой указанной страны (в нашем случае - с Западной Германии) и собирает затем остальные страны в список под названием Закрытый. Каждая страна сначала попадает в другой список, названный Открытый, а потом переносится в Закрытый. Всякий раз, когда страна переносится из Открытый в Закрытый, ее соседи добавляются в Открытый.
создспис( Спис) :-
собрать( [запгермания], [ ], Спис ).
собрать( [ ], Закрытый, Закрытый).
% Кандидатов в Закрытый больше нет
собрать( [X |
Открытый], Закрытый, Спис) :-
принадлежит( Х | Закрытый), !,
% Х уже собран ?
собрaть( Открытый,
Закрытый, Спис).
% Отказаться от Х
собрать( [X |
Открытый], Закрытый, Спис) :-
соседи( X, Соседи),
% Найти соседей Х
конк( Соседи, Открытый, Открытый1),
% Поместить их в Открытый
собрать( Открытый1, [X | Закрытый], Спис).
% Собрать остальные
Отношение конк - как всегда - отношение конкатенации списков.
До сих пор в наших программах конкатенация была определена так:
конк( [ ], L, L).
конк( [X | L1], L2, [X | L3] )
:-
конк( L1, L2, L3 ).
Эта процедура неэффективна, если первый список - длинный. Следующий пример объясняет, почему это так:
?- конк( [а, b, с], [d, e], L).
Этот вопрос порождает следующую последовательность целей:
конк( [а, b, с], [d, e], L)
конк( [b, с], [d, e], L') где L = [a | L']
конк( [с], [d, e], L") где L' = [b | L"]
конк( [ ], [d, e], L'") где L" = [c | L''']
true (истина) где L'" = [d, е]
Ясно, что программа фактически сканирует весь первый список, пока не обнаружит его конец.
А нельзя ли было бы проскочить весь первый список за один шаг и сразу подсоединить к нему второй список, вместо того, чтобы постепенно продвигаться вдоль него? Но для этого необходимо знать, где расположен конец списка, а следовательно, мы нуждаемся в другом его представлении. Один из вариантов - представлять список парой списков. Например, список
[а, b, с]
можно представить следующими двумя списками:
L1 = [a, b, c, d, e]
L2 = [d, e]
[а, b, с]-[ ]
или
[a, b, c, d, e]-[d, e]
или
[a, b, c, d, e | T]-[d, e | T]
или
[а, b, с | Т]-Т
где Т - произвольный список, и т.п. Пустой список представляется любой парой L-L.
Поскольку второй член пары указывает на конец списка, этот конец доступен сразу. Это можно использовать для эффективной реализации конкатенации. Метод показан на рис. 8.1. Соответствующее отношение конкатенации записывается на Прологе в виде факта
конкат( A1-Z1, Z1-Z2, A1-Z2).
Давайте используем конкат для конкатенации двух списков: списка [а, b, с], представленного парой [а, b, с | Т1]-Т1, и списка [d, e], представленного парой [d, e | Т2]-Т2 :
?- конкат( [а, b, с | Т1]-T1, [d, е | Т2]-Т2, L ).
Оказывается, что для выполнения конкатенации достаточно простого сопоставления этой цели с предложением конкат. Результат сопоставления:
T1 = [d, e | Т2]
L = [a, b, c, d, e | T2]-T2

Рис. 8. 1. Конкатенация
списков, представленных в виде разностных пар.
L1 представляется как A1-Z1, L2
как A2-Z2 и результат L3 - как A1-Z2.
При этом должно выполняться равенство Z1 =
А2.
Иногда в процессе вычислений приходится одну и ту же цель достигать снова и снова. Поскольку в Прологе отсутствует специальный механизм выявления этой ситуации, соответствующая цепочка вычислений каждый раз повторяется заново.
В качестве примера рассмотрим программу вычисления N-го числа Фибоначчи для некоторого заданного N. Последовательность Фибоначчи имеет вид:
1, 1, 2, 3, 5, 8, 13, ...
Каждый член последовательности, за исключением первых двух, представляет собой сумму предыдущих двух членов. Для вычисления N-гo числа Фибоначчи F определим предикат
фиб( N, F)
Нумерацию чисел последовательности начнем с N = 1. Программа для фиб обрабатывает сначала первые два числа Фибоначчи как два особых случая, а затем определяет общее правило построения последовательности Фибоначчи:
фиб( 1, 1). % 1-е число Фибоначчи
фиб( 2, 1). % 2-е число Фибоначчи
фиб( N, F) :-
% N-е число Фиб., N > 2
N > 2,
N1 is N - 1, фиб( N1, F1),
N2 is N - 2, фиб( N2, F2),
F is F1 + F2.
%
N-e число есть сумма двух
% предыдущих
Процедура фиб имеет тенденцию к повторению вычислений. Это легко увидеть, если трассировать цель
?- фиб( 6, F).
На рис. 8.2 показано, как протекает этот вычислительный процесс. Например, третье число Фибоначчи f( 3) понадобилось в трех местах, и были повторены три раза одни и те же вычисления.
Этого легко избежать, если запоминать каждое вновь вычисленное число. Идея состоит в применении встроенной процедуры assert для добавления этих (промежуточных) результатов в базу данных в виде фактов. Эти факты должны предшествовать другим предложениям, чтобы предотвратить применение общего правила в случаях, для которых результат уже известен. Усовершенствованная процедура фиб2 отличается от фиб только этим добавлением:
фиб2( 1, 1). % 1-е число Фибоначчи
фиб2( 2, 1). % 2-е число Фибоначчи
фиб2( N, F) :-
% N-e число Фиб., N > 2
N > 2,
Nl is N - 1, фиб2( N1, F1),
N2 is N - 2, фиб2( N2, F2),
F is F1 + F2,
% N-e число есть сумма
% двух предыдущих
asserta( фиб2( N, F) ). %
Запоминание N-го числа
Эта программа, при попытке достичь какую-либо цель, будет смотреть сперва на накопленные об этом отношении факты и только после этого применять общее правило. В результате, после вычисления цели фиб2( N, F), все числа Фибоначчи вплоть до N-го будут сохранены. На рис. 8.3 показан процесс вычислении 6-го числа при помощи фиб2. Сравнение этого рисунка с рис. 8.2. показывает, на сколько уменьшилась вычислительная сложность. Для больших N такое уменьшение еще более ощутимо.
Запоминание промежуточных результатов - стандартный метод, позволяющий избегать повторных вычислений. Следует, однако, заметить, что в случае чисел Фибоначчи повторных вычислений можно избежать еще и применением другого алгоритма, а не только запоминанием промежуточных результатов.
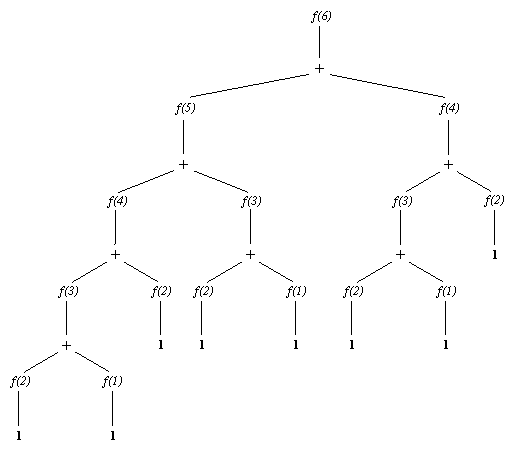
Рис. 8. 2. Вычисление 6-го числа Фибоначчи процедурой фиб.
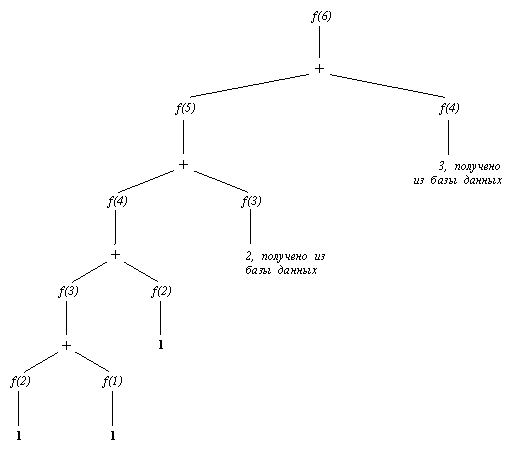
Рис. 8. 3. Вычисление 6-го числа Фибоначчи при помощи процедуры фиб2, которая запоминает предыдущие результаты. По сравнению с процедурой фиб здесь вычислений меньше (см. рис. 8.2).
Этот новый алгоритм позволяет создать программу более трудную для понимания, зато более эффективную. Идея состоит на этот раз не в том, чтобы определить N-e число Фибоначчи просто как сумму своих предшественников по последовательности, оставляя рекурсивным вызовам организовать вычисления "сверху вниз" вплоть до самых первых двух чисел. Вместо этого можно работать "снизу вверх": начать с первых двух чисел и продвигаться вперед, вычисляя члены последовательности один за другим. Остановиться нужно в тот момент, когда будет достигнуто N-e число. Большая часть работы в такой программе выполняется процедурой
фибвперед( М, N, F1, F2, F)
Здесь F1 и F2 - (М - 1)-е и М-е числа, а F - N-e число Фибоначчи. Рис. 8.4 помогает понять отношение фибвперед. В соответствии с этим рисунком фибвперед находит последовательность преобразований для достижения конечной конфигурации (в которой М = N) из некоторой заданной начальной конфигурации. При запуске фибвперед все его аргументы, кроме F, должны быть конкретизированы, а М должно быть меньше или равно N. Вот эта программа:
фиб3( N, F) :-
фибвперед( 2, N, 1, 1, F).
% Первые два числа Фиб. равны 1
фибвперед( М, N, F1, F2,
F2) :-
М >= N. % N-e число достигнуто
фибвперед( M, N, F1, F2, F)
:-
M < N, % N-e число еще не
достигнуто
СледМ is М + 1,
СледF2 is F1 + F2,
фибвперед( СледМ, N, F2, СледF2, F).
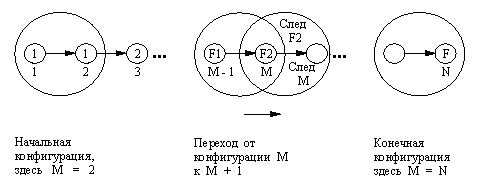
Рис. 8. 4. Отношения в
последовательности Фибоначчи.
"Конфигурация" изображается
здесь в виде большого круга и определяется
тремя параметрами: индексом М и двумя
последовательными числами f( M-1) и f( М).
8. 1. Все показанные ниже процедуры подсп1, подсп2 и подсп3 реализуют отношение взятия подсписка. Отношение подсп1 имеет в значительной мере процедурное определение, тогда как подсп2 и подсп3 написаны в декларативном стиле. Изучите поведение этих процедур на примерах нескольких списков, обращая внимание на эффективность работы. Две из них ведут себя одинаково и имеют одинаковую эффективность. Какие? Почему оставшаяся процедура менее эффективна?
подсп1( Спис,
Подспис) :-
начало( Спис, Подспис).
подсп1( [ _ | Хвост],
Подспис) :-
% Подспис - подсписок хвоста
подсп1( Хвост, Подспис).
начало( _, [ ]).
начало( [X | Спис1], [X |
Спис2] ) :-
начало( Спис1, Спис2).
подсп2( Спис,
Подспис) :-
конк( Спис1, Спис2, Спис),
конк( Спис3, Подспис, Cпис1).
подсп3( Спис,
Подспис) :-
конк( Спис1, Спис2, Спис),
конк( Подспис, _, Спис2).
8. 2. Определите отношение
добавить_в_конец( Список, Элемент, НовыйСписок)
добавляющее Элемент в конец списка Список; результат - НовыйСписок. Оба списка представляйте разностными парами.
8. 3. Определите отношение
обратить( Список, ОбращенныйСписок)
где оба списка представлены разностными парами.
8. 4. Перепищите процедуру собрать из разд. 8.5.2, используя разностное представление списков, чтобы конкатенация выполнялась эффективнее.
Более тонкие и радикальные методы связаны с улучшением алгоритмов (особенно, в части повышения эффективности перебора) и с совершенствованием структур данных.
Назад | Содержание | Вперёд