Назад | Содержание | Вперёд
Сейчас уместно сделать ряд замечаний относительно программ поиска, разработанных к настоящему моменту: во-первых, о поиске в графах, во-вторых, об оптимальности полученных решений и, в-третьих, о сложности поиска.
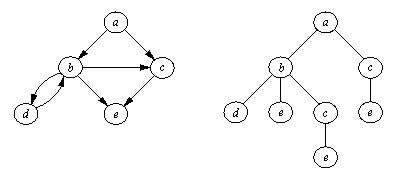
Приведенные примеры могли создать ложное впечатление, что наши программы поиска в ширину способны работать только в пространствах состояний, являющихся деревьями, а не графами общего вида. На самом деле, тот факт, что в одной из версий множество путей-кандидатов представлялось деревом, совсем не означает, что и само пространство состояний должно было быть деревом. Когда поиск проводится в графе, граф фактически разворачивается в дерево, причем некоторые пути, возможно, дублируются в разных частях этого дерева (см. рис. 11.14).
Наши программы поиска в ширину порождают решающие пути один за другим в порядке увеличения их

Рис. 11. 14. (а)
Пространство состояний; а -
стартовая вершина.
(b) Дерево всех возможных
ациклических путей, ведущих из а,
порожденное программой поиска в ширину.
длин - самые короткие решения идут первыми. Это является важным обстоятельством, если нам необходима оптимальность (в отношении длины решения). Стратегия поиска в ширину гарантирует получение кратчайшего решения первым. Разумеется, это неверно для поиска в глубину.
Наши программы, однако, не учитывают стоимости, приписанные дугам в пространстве состояний. Если критерием оптимальности является минимум стоимости решающего пути (а не его длина), то в этом случае поиска в ширину недостаточно. Поиск с предпочтением из гл. 12 будет направлен на оптимизацию стоимости.
Еще одна типичная проблема, связанная с задачей поиска, - это проблема комбинаторной сложности. Для нетривиальных предметных областей число альтернатив столь велико, что проблема сложности часто принимает критический характер. Легко понять, почему это происходит: если каждая вершина имеет b преемников, то число путей длины l, ведущих из стартовой вершины, равно bl ( в предположении, что циклов нет). Таким образом, вместе с увеличением длин путей наблюдается экспоненциальный рост объема множества путей-кандидатов, что приводит к ситуации, называемой комбинаторным взрывом. Стратегии поиска в глубину и ширину недостаточно "умны" для борьбы с такой степенью комбинаторной сложности: отсутствие селективности приводит к тому, что все пути рассматриваются как одинаково перспективные.
По-видимому, более изощренные процедуры поиска должны использовать какую-либо информацию, отражающую специфику данной задачи, с тем чтобы на каждой стадии поиска принимать решения о наиболее перспективных путях поиска. В результате процесс будет продвигаться к целевой вершине, обходя бесполезные пути. Информация, относящаяся к конкретной решаемой задаче и используемая для управления поиском, называется эвристикой. Про алгоритмы, использующие эвристики, говорят, что они руководствуются эвристиками: они выполняют эвристический поиск. Один из таких методов изложен в следующей главе.
Поиск в глубину и поиск в ширину - базовые стратегии поиска, они описаны в любом учебнике по искусственному интеллекту, см., например, Nilsson (1971, 1980) или Winston (1984). Р. Ковальский в своей книге Kowalski (1980) показывает, как можно использовать аппарат математической логики для реализации этих принципов.
Kowalski R. (1980). Logic for Problem Solving. North-Holland.
Nilsson N. J. (1971). Problem Solving Methods in Artificial Intelligence. McGraw-Hill.
Nilsson N. J. (1980). Principles of Artificial Intelligence. Tioga; also Springer- Verlag, 1981.
Winston P. H. (1984). Artificial Intelligence (second edition). Addison-Wesley. [Имеется перевод первого издания: Уинстон П. Искусственный интеллект. - М.: Мир, 1980.]
Назад | Содержание | Вперёд