Назад | Содержание | Вперёд
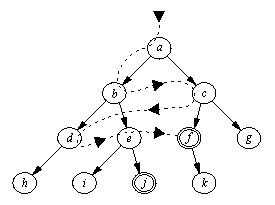
В противоположность поиску в глубину стратегия поиска в ширину предусматривает переход в первую очередь к вершинам, ближайший к стартовой вершине. В результате процесс поиска имеет тенденцию развиваться более в ширину, чем в глубину, что иллюстрирует рис. 11.9.
Поиск в ширину программируется не так легко, как поиск в глубину. Причина состоят в том, что

Рис. 11. 9. Простое
пространство состояний: а -
стартовая вершина,
f и j - целевые вершины. Применение
стратегии поиска в ширину
дает следующий порядок прохода по вершинам:
а, b, c, d, e, f. Более
короткое решение [a, c, f] найдено
раньше, чем более длинное
[а, b, e, j]
нам приходится сохранять все множество альтернативных вершин-кандидатов, а не только одну вершину, как при поиске в глубину. Более того, если мы желаем получить при помощи процесса поиска решающий путь, то одного множества вершин недостаточно. Поэтому мы будем хранить не множество вершин-кандидатов, а множество путей-кандидатов. Таким образом, цель
вширину( Пути, Решения)
истинна только тогда, когда существует путь из множества кандидатов Пути, который может быть продолжен вплоть до целевой вершины. Этот продолженный путь и есть Решение.
В нашей первой реализации этой идеи мы будем использовать следующее представление для множества
решить( Старт,
Решение) :-
вширину( [ [Старт] ], Решение).
вширину( [ [Верш |
Путь] | _ ], [Верш | Путь] ) :-
цель( Верш).
вширину( [ [В | Путь] |
Пути], Решение ) :-
bagof( [B1, В | Путь ],
( после( В, В1), not принадлежит( В1, [В | Путь])),
НовПути),
% НовПути - ациклические продолжения пути [В |
Путь]
конк( Пути, НовПути, Пути1), !,
вширину( Путь1, Решение);
вширину( Пути, Решение).
% Случай, когда у В нет преемника
Рис. 11. 10. Реализации поиска в ширину.
путей-кандидатов. Само множество будет списком путей, а каждый путь - списком вершин, перечисленных в обратном порядке, т. е. головой списка будет самая последняя из порожденных вершин, а последним элементом списка будет стартовая вершина. Поиск начинается с одноэлементного множества кандидатов
[ [СтартВерш] ]
Общие принципы поиска в ширину таковы:
Для того, чтобы выполнить поиск в ширину при заданном множестве путей-кандидатов, нужно:
В случае примера рис.11.9 этот процесс будет развиваться следующим образом:
решить( Старт,
Решение) :-
вширь( [ [Старт] | Z ]-Z, Решение).
вширь( [ [Верш | Путь]
| _ ]-_, [Верш | Путь] ) :-
цель( Верш).
вширь( [ [В | Путь] |
Пути]-Z, Решение ) :-
bagof( [B1, В | Путь ],
( после( В, В1),
not принадлежит( В1, [В | Путь]) ),
Нов ),
конк( Нов, ZZ, Z), !,
вширь( Пути-ZZ, Решение);
Пути \== Z,
% Множество кандидатов не пусто
вширь( Пути-Z, Решение).
Рис. 11. 11. Программа
поиска в ширину более эффективная, чем
программа рис.11.10. Усовершенствование
основано на разностном
представлении списка путей-кандидатов.
(1) Начинаем с начального множества кандидатов:
[ [а] ]
(2) Порождаем продолжения пути [а]:
[ [b, а], [с, а] ]
(Обратите внимание, что пути записаны в обратном порядке.)
(3) Удаляем первый путь из множества кандидатов и порождаем его продолжения:
[ [d, b, a], [e, b, а] ]
Добавляем список продолжений в конец списка кандидатов:
[ [с, а], [d, b, a], [e, b, а] ]
(4) Удаляем [с, а], а затем добавляем все его продолжения в конец множества кандидатов. Получаем:
[ [d, b, a], [e, b, а], [f, c, a], [g, c, a] ]
Далее, после того, как пути [d, b, a] и [e, b, а] будут продолжены, измененный список кандидатов примет вид
[[f, c, a], [g, c, a], [h, d, b, a], [i, e, b, a], [j, e, b, a]]
В этот момент обнаруживается путь [f, c, a], содержащий целевую вершину f. Этот путь выдается в качестве решения.
Программа, порождающая этот процесс, показана на рис. 11.10. В этой программе все продолжения пути на один шаг генерируются встроенной процедурой bagof. Кроме того, делается проверка, предотвращающая порождение циклических путей. Обратите внимание на то, что в случае, когда путь продолжить невозможно, и цель bagof терпит неудачу, обеспечивается альтернативный запуск процедуры вширину. Процедуры принадлежит и конк реализуют отношения принадлежности списку и конкатенации списков соответственно.
Недостатком этой программы является неэффективность операции конк. Положение можно исправить, применив разностное представление списков (см. гл. 8). Тогда множество путей-кандидатов будет представлено парой списков Пути и Z, записанной в виде
Пути-Z
При введении этого представления в программу рис. 11.10 ее можно постепенно преобразовать в программу, показанную на рис. 11.11. Оставим это преобразование читателю в качестве упражнения.
Рассмотрим теперь еще одно изменение нашей программы поиска в ширину. До сих пор мы представляли множества путей-кандидатов как списки путей. Это расточительный способ, поскольку начальные участки путей являются общими для нескольких из них. Таким образом, эти общие части путей приходится хранить во многих экземплярах. Избежать избыточности помогло бы более компактное представление множества кандидатов. Таким более компактным представлением является дерево, в котором общие участки путей хранятся в его верхней части без дублирования. Будем использовать в программе следующее представление дерева. Имеется два случая:
Случай 1: Дерево состоит только из одной вершины В; В этом случае оно имеет вид терма л( В); Функтор л указывает на то, что В - это лист дерева.
Случай 2: Дерево состоит из корневой вершины В и множества поддеревьев Д1, Д2, ... . Такое дерево представляется термом
д( В, Пд)
где Пд - список поддеревьев:
Пд = [ Д1, Д2, ...]
В качестве примера рассмотрим ситуацию, которая возникает после того, как порождены три уровня дерева рис. 11.9. Множество путей-кандидатов в случае спискового представления имеет вид:
[ [d, b, a], [e, b, а], [f, c, a], [g, c, a] ]
В виде дерева это множество выглядит так:
д( а, [д( b, [л( d), л( е)] ), д( с, [л( f), л( g)] )] )
На первый взгляд древовидное представление кажется еще более расточительным, чем списковое, однако это всего лишь поверхностное впечатление, связанное с компактностью прологовской нотации для списков.
В случае спискового представления множества кандидатов эффект распространения процесса в ширину достигался за счет перемещения продолженных путей в конец списка. В нашем случае мы уже не можем использовать этот прием, поэтому программа несколько усложняется. Ключевую роль в нашей программе будет играть отношение
расширить( Путь, Дер, Дер1, ЕстьРеш, Решение)
На рис. 11.12 показано, как связаны между собой аргументы отношения расширить. При каждом обращении к расширить переменные Путь и Дер будут уже конкретизированы. Дер - поддерево всего дерева поиска, одновременно оно служит для представления множества путей-кандидатов внутри этого поддерева. Путь - это путь, ведущий из стартовой вершины в корень поддерева Дер. Самая общая идея алгоритма -
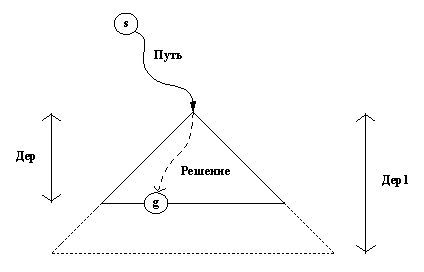
Рис. 11. 12. Отношение paсширить(
Путь, Дер, Дер1, ЕстьРеш, Решение):
s - стартовая вершина, g
- целевая вершина. Решение - это Путь,
продолженный вплоть до g. Дер1
- результат расширения дерева
Дер на один уровень вниз.
получить поддерево Дер1 как результат расширения Дер на один уровень. Но в случае, когда в процессе расширения поддерева Дер встретится целевая вершина, процедура расширить должна сформировать соответствующий решающий путь.
Итак, процедура расширить будет порождать два типа результатов. На конкретный вид результата будет указывать значение переменной ЕстьРеш:
(1) ЕстьРеш = да
Решение
= решающий путь, т. е. Путь, продолженный
до целевой вершины.
Дер1
= неконкретизировано.
Разумеется, такой тип результата получится только в том случае, когда Дер будет содержать целевую вершину. Добавим также, что эта целевая вершина обязана быть листом поддерева Дер.
(2) ЕстьРеш = нет
Дер1
= результат расширения поддерева Дер на
один уровень вниз от своего "подножья". Дер1
не содержит ни одной "тупиковой" ветви из Дер,
т. е. такой ветви, что она либо не может быть
продолжена из-за отсутствия преемников, либо
любое ее продолжение приводит к циклу.
Решение
= неконкретизировано.
Если в дереве Дер нет ни одной целевой вершины и, кроме того, оно не может быть расширено, то процедура расширить терпит неудачу.
Процедура верхнего уровня для поиска в ширину
вширину( Дер, Решение)
отыскивает Решение либо среди множества кандидатов Дер, либо в его расширении. На рис. 11.3 показано, как выглядит программа целиком. В этой программе имеется вспомогательная процедура расширитьвсе. Она расширяет все деревья из некоторого списка, и затем, выбросив все "тупиковые" деревья", собирает все полученные расширенные деревья в один новый список. Используя механизм возвратов, она также порождает все решения, обнаруженные в деревьях из списка. Имеется одна дополнительная деталь: по крайней мере одно из деревьев должно "вырасти". Если это не так, то процедуре расширитьвсе не удается получить ни одного расширенного дерева - все деревья из списка оказываются "тупиковыми".
% ПОИСК В ШИРИНУ
% Множество кандидатов представлено деревом
решить( Старт,
Решение) :-
вширину( л( Старт), Решение).
вширину( Дер,
Решение) :-
расширить( [ ], Дер, Дер1, ЕстьРеш, Решение),
( ЕстьРеш = да;
ЕстьРеш = нет, вширину( Дер1, Решение) ).
расширить( П, Л( В), _,
да, [В | П] ) :-
цель( В).
расширить( П, Л( В), д(
В, Пд), нет, _ ) :-
bagof( л( B1),
( после( В, B1), not принадлежит( В1, П)), Пд).
расширить( П, д( В,
Пд), д( В, Пд1), ЕстьРеш, Реш) :-
расширитьвсе( [В | П], Пд, [ ], Пд1, ЕстьРеш, Реш).
расширитьвсе( _, [ ],
[Д | ДД], [Д | ДД], нет, _ ).
% По крайней мере одно дерево должно вырасти
расширитьвсе( П, [Д |
ДД], ДД1, Пд1, ЕстьРеш, Реш) :-
расширить ( П, Д, Д1, ЕстьРеш1, Реш),
( ЕстьРеш 1= да, ЕстьРеш = да;
ЕстьРеш1 = нет, !,
расширитьвсе( П, ДД, [Д1 | ДД1], Пд1, ЕстьРеш, Реш));
расширитьвсе( П, ДД, ДД1, Пд1, ЕстьРеш, Реш ).
Рис. 11. 13. Реализация
поиска в ширину с использованием
древовидного представления множества
путей-кандидатов.
Мы разработали эту более сложную реализацию поиска в ширину не только для того, чтобы получать программу более экономичную по сравнению с предыдущей версией, но также и потому, что такое решение задачи может послужить хорошим стартом для перехода к усложненным программам поиска, управляемым эвристиками, таким как программа поиска с предпочтением из гл. 12.
11. 5. Перепишите программу поиска в ширину рис. 11.10, используя разностное представление для списка путей-кандидатов и покажите, что в результате получится программа, приведенная на рис. 11.11. Зачем в программу рис. 11.11 включена цель
Пути \== Z
Проверьте, что случится при поиске в пространстве состояний рис. 11.9, если эту цель опустить. Различие в выполнении программы, возникнет только при попытке найти новые решения в ситуации, когда не осталось больше ни одного решения.
11. 6. Как программы настоящего раздела можно использовать для поиска, начинающегося от стартового множества вершин, вместо одной стартовой вершины?
11. 7. Как программы этой главы можно использовать для поиска в обратном направлении, т.е. от целевой вершины к стартовой вершине (или к одной из стартовых вершин, если их несколько). Указание: переопределите отношение после. В каких ситуациях обратный поиск будет иметь преимущества перед прямым поиском?
11. 8. Иногда выгодно сделать поиск двунаправленным, т. е. продвигаться одновременно с двух сторон от стартовой и целевой вершин. Поиск заканчивается, когда оба пути "встречаются". Определите пространство поиска (отношение после) и целевое отношение для заданного графа таким образом, чтобы наши процедуры поиска в действительности выполняли двунаправленный поиск.
11. 9. Проведите эксперименты с различными методами поиска применительно к задаче планирования в "мире кубиков".
Назад | Содержание | Вперёд