Пример. Теперь можно приступить к реализации операции пересечения двух множеств. Напомним, что пересечение двух множеств — это множество, образованное элементами, которые одновременно принадлежат и первому, и второму множествам. Обозначается пересечение множеств A и B через A B. В математических обозначениях это выглядит следующим образом: A
B. В математических обозначениях это выглядит следующим образом: A B={x|x
B={x|x A и x
A и x B}. На рисунке пересечение множеств A и B обозначено штриховкой.
B}. На рисунке пересечение множеств A и B обозначено штриховкой.
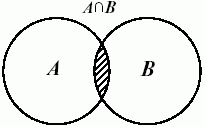
Рис. 9.2.
Пересечение множеств A и B
У предиката, реализующего эту операцию, как и у предиката, осуществляющего объединение двух множеств, есть три параметра: первые два — исходные множества, третий — результат пересечения двух первых аргументов. В итоговом множестве должны оказаться те элементы, которые входят и в первое, и во второе множество одновременно.
Этот предикат, наверное, будет немного проще объединения. Его мы также проведем рекурсией по первому множеству. Базис рекурсии: пересечение пустого множества с любым множеством будет пустым множеством. Шаг рекурсии так же, как и в случае объединения, разбивается на два случая в зависимости от того, принадлежит ли первый элемент первого множества второму. В ситуации, когда голова первого множества является элементом второго множества, пересечение множеств получается приписыванием головы первого множества к пересечению хвоста первого множества со вторым множеством. В случае, когда первый элемент первого множества не встречается во втором множестве, результирующее множество получается пересечением хвоста первого множества со вторым множеством.
Запишем это.
intersection([],_,[]). /* в результате пересечения
пустого множества с любым
множеством получается пустое
множество */
intersection([H|T1],S2,[H|T]):–
member3(H,S2),
/* если голова первого множества H
принадлежит второму множеству S2 */
!,
intersection(T1,S2,T).
/* то результатом будет множество,
образованное головой первого
множества H и хвостом, полученным
пресечением хвоста первого
множества T1 со вторым
множеством S2 */
intersection([_|T],S2,S):–
intersection(T,S2,S).
/* в противном случае результатом
будет множество S, полученное
объединением хвоста первого
множества T со вторым
множеством S2 */
Если пересечь множество [1,2,3,4] со множеством [3,4,5], то в результате получится множество [3,4].
Пример. Следующая операция, которую стоит реализовать, — это разность двух множеств. Напомним, что разность двух множеств — это множество, образованное элементами первого множества, не принадлежащими второму множеству. Обозначается разность множеств A и B через A–B или A\B. В математических обозначениях это выглядит следующим образом: A\B={x|x A и х
A и х B}.
B}.
На рисунках разность множеств A и B (B и A) обозначена штриховкой.
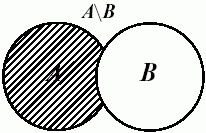
Рис. 9.3.
Разность множеств A и B
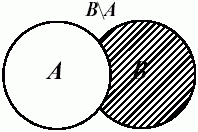
Рис. 9.4.
Разность множеств В и А
В этой операции, в отличие от двух предыдущих, важен порядок множеств. Если в объединении или пересечении множеств поменять первый и второй аргументы местами, результат останется прежним. В то время как при A={1,2,3,4}, B={3,4,5}, A\B={1,2}, но B\A={5}.
У предиката, реализующего разность, как и у объединения и пересечения, будет три аргумента: первый — множество, из которого нужно вычесть, второй — множество, которое нужно отнять, третий — результат вычитания из первого аргумента второго. В третий параметр должны попасть те элементы первого множества, которые не принадлежат второму множеству.
Рекурсия по первому множеству поможет нам реализовать вычитание. В качестве базиса рекурсии возьмем очевидный факт: при вычитании произвольного множества из пустого множества ничего кроме пустого множества получиться не может, так как в пустом множестве элементов нет. Шаг рекурсии, как и в случае объединения и пересечения, зависит от того, принадлежит ли первый элемент множества, из которого вычитают, множеству, которое вычитают. В случае, когда голова первого множества является элементом второго множества, разность множеств получается путем вычитания второго множества из хвоста первого. Когда первый элемент множества, из которого производится вычитание, не встречается в вычитаемом множестве, ответом будет множество, образованное приписыванием головы первого множества к результату вычитания второго множества из хвоста первого множества.
Запишем эти рассуждения.
minus([],_,[]). /* при вычитании любого множества
из пустого множества получится пустое
множество */
minus([H|T],S2,S):–
member3(H,S2),
/* если первый элемент первого
множества H принадлежит второму
множеству S2*/
!,
minus(T,S2,S).
/* то результатом S будет разность
хвоста первого множества T
и второго множества S2 */
minus([H|T],S2,[H|S]):–
minus(T,S2,S).
/* в противном случае, результатом
будет множество, образованное
первым элементом первого
множества H и хвостом, полученным
вычитанием из хвоста первого
множества T второго множества S2 */
Можно попробовать реализовать пересечение через разность. Из математики нам известно тождество A B=A\(A\B). Попробуем проверить это тождество, записав соответствующий предикат, реализующий пересечение множеств, через взятие разности.
B=A\(A\B). Попробуем проверить это тождество, записав соответствующий предикат, реализующий пересечение множеств, через взятие разности.
intersection2(A,B,S):–
minus(A,B,A_B), /*A_B=A\B */
minus(A,A_B,S). /* S = A\A_B = A\(A\B) */
Проверка на примерах показывает, что этот предикат, так же, как, впрочем, и ранее созданный предикат intersection, возвращает именно те результаты, которые ожидаются.
