Данная лекция будет посвящена изучению и реализации на Прологе такой структуры данных, как деревья .

Начнем с маленького введения из теории графов , частным случаем которых являются деревья .

Обычно графом называют пару множеств: множество вершин и множество дуг (множество пар из множества вершин).Различают ориентированные и неориентированные графы . В ориентированном графе каждая дуга имеет направление (рассматриваются упорядоченные пары вершин). Графически обычно принято изображать вершины графа точками, а связи между ними - линиями, соединяющими точки-вершины.

Путем называется последовательность вершин, соединенных дугами. Для ориентированного графа направление пути должно совпадать с направлением каждой дуги, принадлежащей пути . Циклом называется путь , у которого совпадают начало и конец.

Две вершины ориентированного графа , соединенные дугой, называются отцом и сыном (или главной и подчиненной вершинами). Известно, что если граф не имеет циклов , то обязательно найдется хотя бы одна вершина, которая не является ничьим сыном. Такую вершину называют корневой. Если из одной вершины достижима другая, то первая называется предком , вторая - потомком .

Деревом называется граф , у которого одна вершина корневая, остальные вершины имеют только одного отца и все вершины являются потомками корневой вершины.

Листом дерева называется его вершина, не имеющая сыновей. Кроной дерева называется совокупность всех листьев . Высотой дерева называется наибольшая длина пути от корня к листу .

Нам будет удобно использовать следующее рекурсивное определение бинарного дерева : дерево либо пусто, либо состоит из корня , а также левого и правого поддеревьев, которые в свою очередь также являются деревьями .

В вершинах дерева может храниться информация любого типа. Для простоты в этой лекции будем считать, что в вершинах дерева располагаются целые числа. Тогда соответствующее этому определению описание альтернативного домена будет выглядеть следующим образом:

DOMAINS
tree=empty;tr(i,tree,tree) 
        /* дерево либо пусто, либо 
         состоит из корня (целого числа), 
         левого и правого поддеревьев, 
         также являющихся деревьями */

Заметим, что идентификатор empty не является зарезервированным словом Пролога. Вместо него вполне можно употреблять какое-нибудь другое обозначение для пустого дерева . Например, можно использовать для обозначения дерева , не имеющего вершин, идентификатор nil, как в Лиспе, или void, как в Си. То же самое относится и к имени домена (и имени функтора): вместо tree (tr) можно использовать любой другой идентификатор.

Например, дерево

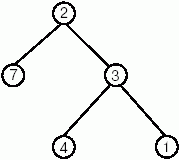
можно задать следующим образом:

tr(2,tr(7,empty, empty),tr(3,tree(4,empty,empty),
 tr(1,empty,empty))).

Теперь займемся написанием предикатов для реализации операций на бинарных деревьях .

Пример. Начнем с реализации предиката, который будет проверять принадлежность значения дереву . Предикат будет иметь два аргумента. Первым аргументом будет исходное значение, вторым - дерево , в котором мы ищем данное значение.

Следуя рекурсивному определению дерева , заметим, что некоторое значение принадлежит данному дереву , если оно либо содержится в корне дерева , либо принадлежит левому поддереву, либо принадлежит правому поддереву. Других вариантов нет.

Запишем это рассуждение на Прологе.

tree_member(X,tr(X,_,_)):-!. /* X - является корнем 
            дерева */
tree_member(X,tr(_,L,_)):-
     tree_member(X,L),!. /* X принадлежит 
              левому поддереву */
tree_member(X,tr(_,_,R)):-
     tree_member(X,R). /* X принадлежит 
             правому поддереву */

Пример. Разработаем предикат, который будет заменять в дереве все вхождения одного значения на другое. У предиката будет четыре аргумента: три входных (значение, которое нужно заменять; значение, которым нужно заменять; исходное дерево ), четвертым - выходным - аргументом будет дерево , полученное в результате замены всех вхождений первого значения на второе.

Базис рекурсивного решения будет следующий. Из пустого дерева можно получить только пустое дерево . При этом абсолютно неважно, что на что мы заменяем. Шаг рекурсии зависит от того, находится ли заменяемое значение в корне дерева . Если находится, то нужно заменить корневое значение вторым значением, после чего перейти к замене первого значения на второе в левом и правом поддереве. Если же в корне содержится значение, отличное от заменяемого, то оно должно остаться. Замену нужно произвести в левом и правом поддеревьях.

tree_replace(_,_,empty,empty). /* пустое дерево 
              остается пустым деревом*/
tree_replace(X,Y,tr(X,L,R),tr(Y,L1,R1)):- 
          /* корень содержит заменяемое 
            значение X*/
      !,tree_replace(X,Y,L,L1), 
          /* L1 - результат замены 
            в дереве L всех вхождений X 
            на Y */
      tree_replace(X,Y,R,R1). 
          /* R1 - результат замены 
            в дереве R всех вхождений X 
            на Y */
tree_replace(X,Y,tr(K,L,R),tr(K,L1,R1)):- 
          /* корень не содержит 
            заменяемое значение X */
      tree_replace(X,Y,L,L1), 
          /* L1 - результат замены 
            в дереве L всех вхождений X 
            на Y */
      tree_replace(X,Y,R,R1). 
          /* R1 - результат замены 
            в дереве R всех вхождений X 
            на Y */