Назад | Содержание | Вперёд
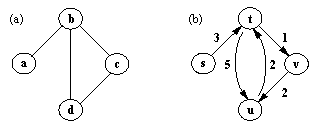
Графы используются во многих приложениях, например для представления отношений, ситуаций или структур задач. Граф определяется как множество вершин вместе с множеством ребер, причем каждое ребро задается парой вершин. Если ребра направлены, то их также называют дугами. Дуги задаются упорядоченными парами. Такие графы называются направленными. Ребрам можно приписывать стоимости, имена или метки произвольного вида, в зависимости от конкретного приложения. На рис. 6.18 показаны примеры графов.
В Прологе графы можно представлять различными способами. Один из них - каждое ребро записывать в виде отдельного предложения. Например, графы, показанные иа рис. 9.18, можно представить в виде следующего множества предложений:
связь( а, b).
связь( b, с).
. . .
дуга( s, t, 3).
дуга( t, v, 1).
дуга( u, t, 2).
. . .
Другой способ - весь граф представлять как один объект. В этом случае графу соответствует пара множеств - множество вершин и множество ребер. Каждое множество можно задавать при помощи списка, каждое ребро - парой вершин. Для объединения двух множеств в пару будем применять функтор граф, а для записи ребра - функтор р. Тогда (ненаправленный) граф рис. 9.18 примет вид:
G1 = граф( [a, b, c, d],
[р(
а, b), р( b, d), р( b, с), p( c, d)] )

Рис. 9. 18. (а) Граф. (b) Направленный граф. Каждой дуге приписана ее стоимость.
Для представления направленного графа (рис. 9.18), применив функторы диграф и д (для дуг), получим
G2 = диграф( [s, t, u, v],
[д( s, t, 3), д( t, v, 1), д( t, u, 5), д( u, t, 2),
д(
v, u, 2) ] )
Если каждая вершина графа соединена ребром еще по крайней мере с одной вершиной, то в представлении графа можно опустить множество вершин, поскольку оно неявным образом содержится в списке ребер.
Еще один способ представления графа - связать с каждой вершиной список смежных с ней вершин. В этом случае граф превращается в список пар, каждая из которых состоит из вершины- плюс ее список смежности. Наши графы (рис. 9.18), например, можно представить как
G1 = [ a->[b1, b->[a, c, d], c->[b, d], d->[b, c] ]
G2 = [s->[t/3], t->[u/5, v/l], u->[t/2], v->[u/2]]
Здесь символы '->' и '/' - инфиксные операторы.
Какой из способов представления окажется более удобным, зависит от конкретного приложения, а также от того, какие операции имеется в виду выполнять над графами. Вот типичные операции:
Примером последней операции может служить построение основного дерева графа. В последующих разделах, мы рассмотрим некоторые простые программы для поиска пути в графе и построения основного дерева.
Пусть G - граф, а А и Z - две его вершины. Определим отношение
путь( А, Z, G, Р)
где Р - ациклический путь между А и Z в графе G. Если G - граф, показанный в левой части рис. 9.18, то верно:
путь( a, d, G, [a, b, d] )
путь( а, d, G, [a, b, c, d] )
Поскольку путь не должен содержать циклов, любая вершина может присутствовать в пути не более одного раза. Вот один из методов поиска пути:
Для того, чтобы найти ациклический путь Р между А и Z в графе G, необходимо:
Если А = Z , то положить Р = [А], иначе найти ациклический путь Р1 из произвольной вершины Y в Z, а затем найти путь из А в Y, не содержащий вершин из Р1.
В этой формулировке неявно предполагается, что существует еще одно отношение, соответствующее поиску пути со следующий ограничением: путь не должен проходить через вершины из некоторого подмножества (в данном случае Р1) множества всех вершин графа. В связи с этим мы определим ещё одну процедуру:
путь1( А, Р1, G, Р)
Аргументы в соответствии с рис. 9.19 имеют следующий смысл:
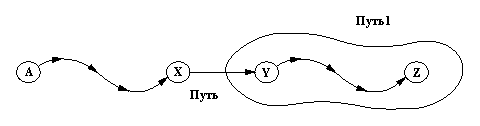
Pис. 9. 19. Отношение путь1:
Путь - это путь между А и Z,
в своей
заключительной части он перекрывается с Путь1.
Между путь и путь1 имеется следующее соотношение:
путь( А, Z, G, Р) :- путь1( А, [Z], G, Р).
На рис. 9.19 показана идея рекурсивного определения отношения путь1. Существует "граничный" случай, когда начальная вершина пути P1 (Y на рис. 9.19) совпадает с начальной вершиной А пути Р. Если же начальные вершины этих двух путей не совпадают, то должна существовать такая вершина X, что
(1) Y - вершина, смежная с X,
(2) Х не содержится в Р1 и
(3) для Р выполняется
отношение
путь1( А,
[Х | Р1], G, Р).
путь( A, Z, Граф, Путь)
:-
путь1( А, [Z], Граф, Путь).
путь1( А, [А | Путь1, _, [А | Путь1] ).
путь1( А, [Y | Путь1],
Граф, Путь) :-
смеж( X, Y, Граф),
принадлежит( X, Путь1),
% Условие отсутствия цикла
путь1( А, [ X, Y | Путь1], Граф, Путь).
Рис. 9. 20. Поиск в графе Граф ациклического пути Путь из А в Z.
На рис. 9.20 программа показана полностью. Здесь принадлежит - отношение принадлежности элемента списку. Отношение
смеж( X, Y, G)
означает, что в графе G существует дуга, ведущая из Х в Y. Определение этого отношения зависит от способа представления графа. Если G представлен как пара множеств (вершин и ребер)
G = граф( Верш, Реб)
то
смеж( X, Y, граф( Верш,
Реб) ) :-
принадлежит( р( X, Y), Реб);
принадлежит( р( Y, X), Реб).
Классическая задача на графах - поиск Гамильтонова цикла, т.е. ациклического пути, проходящего через все вершины графа. Используя отношение путь, эту задачу можно решить так:
гамильтон( Граф,
Путь) :-
путь( _, _, Граф, Путь),
всевершины( Путь, Граф).
всевершины( Путь,
Граф) :-
not (вершина( В, Граф),
not принадлежит( В, Путь) ).
Здесь вершина( В, Граф) означает: В - вершина графа Граф.
Каждому пути можно приписать его стоимость. Стоимость пути равна сумме стоимостей входящих в него дуг. Если дугам не приписаны стоимости, то тогда, вместо стоимости, говорят о длине пути.
Для того, чтобы наши отношения путь и путь1 могли работать со стоимостями, их нужно модифицировать, введя дополнительный аргумент для каждого пути:
путь( А, Z, G, Р, С)
путь1( A, P1, C1, G, Р, С)
Здесь С - стоимость пути Р, a C1 - стоимость пути Р1. В отношении смеж также появится дополнительный аргумент, стоимость дуги. На рис. 9.21 показана программа поиска пути, которая строит путь и вычисляет его стоимость.
путь( А, Z, Граф, Путь,
Ст) :-
путь1( A, [Z], 0, Граф, Путь, Ст).
путь1( А, [А | Путь1], Ст1, Граф, [А | Путь1], Ст).
путь1( А, [Y | Путь1],
Ст1, Граф, Путь, Ст) :-
смеж( X, Y, СтXY, Граф),
not принадлежит( X, Путь1),
Ст2 is Ст1 + СтXY,
путь1( А, [ X, Y | Путь1], Ст2, Граф, Путь, Ст).
Рис. 9. 21. Поиск пути в графе: Путь - путь между А и Z в графе Граф стоимостью Ст.
Эту процедуру можно использовать для нахождения пути минимальной стоимости. Мы можем построить путь минимальной стоимости между вершинами Верш1, Верш2 графа Граф, задав цели
путь( Bepш1, Верш2,
Граф, МинПуть, МинСт),
not ( путь( Верш1, Верш2, Граф,
_, Ст), Ст<МинСт )
Аналогично можно среди всех путей между вершинами графа найти путь максимальной стоимости, задав цели
путь( _, _, Граф,
МаксПуть, МаксСт),
not ( путь( _, _, Граф, _, Ст), Ст
> МаксСт)
Заметим, что приведенный способ поиска максимальных и минимальных путей крайне неэффективен, так как он предполагает просмотр всех возможных путей и потому не подходит для больших графов из-за своей высокой временной сложности. В искусственном интеллекте задача поиска пути возникает довольно часто. В главах 11 и 12 мы изучим более сложные методы нахождения оптимальных путей.
Граф называется связным, если между любыми двумя его вершинами существует путь. Пусть G = (V, Е) - связный граф с множеством вершин V и множеством ребep Е. Остовное дерево графа G - это связный граф Т = ( V, Е'), где Е' - подмножество Е такое, что
(1) Т - связный граф,
(2) в Т нет циклов.
Выполнение этих двух условий гарантирует то, что Т - дерево. Для графа, изображенного в левой части рис. 9.18, существует три остовных дерева, соответствующих следующим трем спискам ребер:
Дер1 = [а-b, b-c, c-d]
Дер2 = [а-b, b-d, d-с]
Дер3 = [а-b, b-d, b-c]
Здесь каждый терм вида X-Y обозначает ребро, соединяющее вершины Х и Y. В качестве корня можно взять любую из вершин, указанных в списке. Остовные деревья представляют интерес, например в задачах проектирования сетей связи, поскольку они позволяют, имея минимальное число линий, установить связь между любыми двумя узлами, соответствующими вершинам графа.
Определим процедуру
остдерево( G, Т)
где Т - остовное дерево графа G. Будем предполагать, что G - связный граф. Можно представить себе алгоритмический процесс построения остовного дерева следующим образом. Начать с пустого множества ребер и постепенно добавлять новые ребра, постоянно следя за тем, чтобы не образовывались циклы. Продолжать этот процесс до тех пор, пока не обнаружится, что нельзя присоединить ни одного ребра, поскольку любое новое ребро порождает цикл. Полученное множество ребер будет остовным деревом. Отсутствие циклов можно обеспечить, если придерживаться следующего простого правила: ребро присоединяется к дереву только в том случае, когда одна из его вершин уже содержится в строящемся дереве, а другая пока еще не включена в него. Программа, реализующая эту идею, показана на рис. 9.22. Основное отношение, используемое в этой программе, - это
расширить( Дер1, Дер, G)
Здесь все три аргумента - множества ребер. G -
% Построение остовного дерева
графа
%
% Деревья и графы представлены списками
% своих ребер, например:
% Граф = [а-b,
b-с, b-d, c-d]
остдерево( Граф,
Дер) :-
% Дер - остовное дерево
Граф'а
принадлежит( Ребро, Граф),
расширить( [Ребро], Дер, Граф).
расширить( Дер1, Дер,
Граф) :-
добребро( Дер1, Дер2, Граф),
расширить( Дер2, Дер, Граф).
расширить( Дер, Дер,
Граф) :-
not добребро( Дер, _, Граф).
% Добавление любого ребра приводит к циклу
добребро( Дер, [А-В |
Дер], Граф) :-
смеж( А, В, Граф),
% А и В - смежные вершины
вершина( А, Дер).
% А содержится в Дер
не вершина( В, Дер).
% А-В не порождает цикла
смеж( А, В, Граф) :-
принадлежит ( А-В, Граф);
принадлежит ( В-А, Граф).
вершина( А, Граф) :-
% А содержится в графе, если
смеж( А, _, Граф).
% А смежна какой-нибудь вершине
Pис. 9. 22. Построение
остовного дерева: алгоритмический подход.
Предполагается, что Граф - связный
граф.
связный граф; Дер1 и Дер - два подмножества G, являющиеся деревьями. Дер - остовное дерево графа G, полученное добавлением некоторого (может быть пустого) множества ребер из G к Дер1. Можно сказать, что "Дер1 расширено до Дер".
Интересно, что можно написать программу построения остовного дерева совершенно другим, полностью декларативным способом, просто формулируя на Прологе некоторые математические определения. Допустим, что как графы, так и деревья задаются списками своих ребер, как в программе рис. 9.22. Нам понадобятся следующие определения:
(1) Т является остовным деревом графа G, если
(2) Множество ребер Т есть дерево, если
Эти определения можно сформулировать на Прологе (с использованием нашей программы путь из предыдущего раздела) так, как показано на рис. 9.23. Следует, однако, заметить, что эта программа в таком ее виде не представляет практического интереса из-за своей неэффективности.
% Построение остовного дерева
% Графы и деревья представлены списками ребер.
остдерево( Граф,
Дер) :-
подмнож( Граф, Дер),
дерево( Дер),
накрывает( Дер, Граф).
дерево( Дер) :-
связи( Дер),
not имеетцикл( Дер).
связи( Дер) :-
not ( вершина( А, Дер), вершина( В, Дер),
not путь( А, А, Дер, _ ) ).
имеетцикл( Дер) :-
смеж( А, В, Дер),
путь( А, В, Дер, [А, X, Y | _ ).
% Длина пути > 1
накрывает( Дер,
Граф) :-
not ( вершина( А, Граф), not вершина( А, Дер) ).
подмнож( [ ], [ ]).
подмнож( [ Х | L], S) :-
подмнож( L, L1),
( S = L1; S = [ Х | L1] ).
Рис. 9. 23. Построение
остовного дерева: "декларативный подход".
Отношения вершина и смеж
см. на рис. 9. 22.
9. 15. Рассмотрите остовные деревья в случае, когда каждому ребру графа приписана его стоимость. Пусть стоимость остовного дерева определена как сумма стоимостей составляющих его ребер. Напишите программу построения для заданного графа его остовного дерева минимальной стоимости.
В данной главе мы изучали реализацию на Прологе некоторых часто используемых структур данных и соответствующих операций над ними. В том числе
В этой главе мы занимались такими важными темами, как сортировка и работа со структурами данных для представления множеств. Общее описание структур данных, а также алгоритмов, запрограммированных в данной главе, можно найти, например, в Aho, Hopcroft and Ullman (1974, 1983) или Baase (1978). В литературе рассматривается также поведение этих алгоритмов, особенно их временная сложность. Хороший и краткий обзор соответствующих алгоритмов и результатов их математического анализа можно найти в Gonnet (1984).
Прологовская программа для внесения нового элемента на произвольный уровень дерева (раздел 9.3) была впервые показана автору М. Ван Эмденом (при личном общении).
Aho А. V., Hopcroft J. Е. and Ullman J. D. (1974). The Design and Analysis of Computer Algorithms. Addison-Wesley. [Имеется перевод: Ахо А., Хопкрофт Дж. Построение и анализ вычислительных алгоритмов. Пер. с англ. - М-: Мир, 1979.]
Aho А. V., Hopcroft J. Е. and Ullman J. D. (1983). Data Structures and Algorithms. Addison-Wesley.
Baase S. (1978). Computer Algorithms. Addison-Wesley.
Gonnet G. H. (1984). Handbook of Algorithms and Data Structures. Addison-Wesley.
Назад | Содержание | Вперёд