Назад | Содержание | Вперёд
Данное упражнение показывает, как абстрактную математическую конструкцию можно представить на Прологе. Кроме того, программа, которая получится, окажется значительно более гибкой, чем предполагалось вначале.
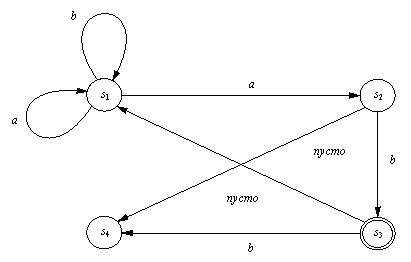
Недетерминированный конечный автомат - это абстрактная машина, которая читает символы из входной цепочки и решает, допустить или отвергнуть эту цепочку. Автомат имеет несколько состояний и всегда находится в одном из них. Он может изменить состояние, перейдя из одного состояния в другое. Внутреннюю структуру такого автомата можно представить графом переходов, как показано на рис. 4.3. В этом примере S1, S2, S3 и S4 - состояния автомата. Стартовав из начального состояния (в нашем примере это S1 ), автомат переходит из состояния в состояние по мере чтения входной цепочки. Переход зависит от текущего входного символа, как указывают метки на дугах графа переходов.

Рис. 4. 3. Пример недетерминированного конечного автомата.
Переход выполняется всякий раз при чтении входного символа. Заметим, что переходы могут быть недетерминированными. На рис. 4.3 видно, что если автомат находится в состоянии S1, и текущий входной символ равен а, то переход может осуществиться как в S1, так и в S2. Некоторые дуги помечены меткой пусто, обозначающей "пустой символ". Эти дуги соответствуют "спонтанным переходам" автомата. Такой переход называется спонтанным, потому что он выполняется без чтения входной цепочки. Наблюдатель, рассматривающий автомат как черный ящик, не сможет обнаружить, что произошел какой-либо переход.
Состояние S3 обведено двойной линией, это означает, что S3 - конечное состояние. Про автомат говорят, что он допускает входную цепочку, если в графе переходов существует путь, такой, что:
(1) он начинается в
начальном состоянии,
(2) он оканчивается в
конечном состоянии, и
(3) метки дуг, образующих
этот путь, соответствуют полной входной цепочке.
Решать, какой из возможных переходов делать в каждый момент времени - исключительно внутреннее дело автомата. В частности, автомат сам решает, делать ли спонтанный переход, если он возможен в
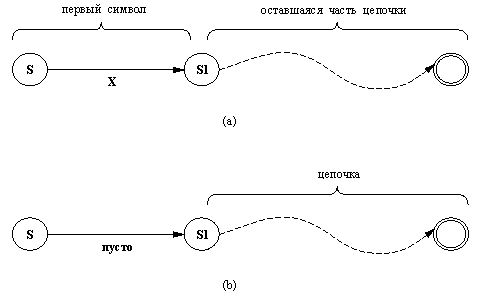
Рис. 4. 4. Допущение
цепочки: (a) при чтении первого
символа X;
(b) при совершении спонтанного
перехода.
текущем состоянии. Однако абстрактные недетерминированные машины такого типа обладают волшебным свойством: если существует выбор, они всегда избирают "правильный" переход, т.е. переход, ведущий к допущению входной цепочки при наличии такого перехода. Автомат на рис. 4.3, например, допускает цепочки аb и aabaab, но отвергает цепочки abb и abba. Легко видеть, что этот автомат допускает любые цепочки, оканчивающиеся на аb и отвергает все остальные.
Некоторый автомат можно описать на Прологе при помощи трех отношений:
(1) Унарного отношения конечное, которое определяет конечное состояние автомата.
(2) Трехаргументного отношения переход, которое определяет переход из состояния в состояние, при этом
переход( S1, X, S2)
означает переход из состояния S1 в S2, если считан входной символ X.
(3) Бинарного отношения
спонтанный( S1, S2)
означающего, что возможен спонтанный переход из S1 в S2.
Для автомата, изображенного на рис. 4.3, эти отношения будут такими:
конечное( S3).
переход( S1, а, S1).
переход( S1, а, S2).
переход( S1, b, S1).
переход( S2, b, S3).
переход( S3, b, S4).
спонтанный( S2, S4).
спонтанный( S3, S1).
Представим входные цепочки в виде списков Пролога. Цепочка ааb будет представлена как [а, а, b]. Модель автомата, получив его описание, будет обрабатывать заданную входную цепочку, и решать, допускать ее или нет. По определению, недетерминированный автомат допускает заданную цепочку, если (начав из начального состояния) после ее прочтения он способен оказаться в конечном состоянии. Модель программируется в виде бинарного отношения допускается, которое определяет принятие цепочки из данного состояния. Так
допускается( Состояние, Цепочка)
истинно, если автомат, начав из состояния Состояние как из начального, допускает цепочку Цепочка. Отношение допускается можно определить при помощи трех предложений. Они соответствуют следующим трем случаям:
(1) Пустая цепочка [ ] допускается из состояния S, если S - конечное состояние.
(2) Непустая цепочка допускается из состояния S, если после чтения первого ее символа автомат может перейти в состояние S1, и оставшаяся часть цепочки допускается из S1. Этот случай иллюстрируется на рис. 4.4(а).
(3) Цепочка допускается из состояния S, если автомат может сделать спонтанный переход из S в S1, а затем допустить (всю) входную цепочку из S1. Такой случай иллюстрируется на рис. 4.4(b).
Эти правила можно перевести на Пролог следующим образом:
допускается( S, [ ]) :-
% Допуск пустой цепочки
конечное(
S).
допускается( S, [X |
Остальные]) :-
% Допуск чтением первого символа
переход(
S, X, S1),
допускается( S1, Остальные).
допускается( S,
Цепочка) :-
% Допуск выполнением спонтанного перехода
спонтанный(
S, S1),
допускается( S1, Цепочка).
Спросить о том, допускается ли цепочка аааb, можно так:
?- допускается( S1, [a, a, a, b]).
yes (да)
Как мы уже видели, программы на Прологе часто оказываются способными решать более общие задачи, чем те, для которых они первоначально предназначались. В нашем случае мы можем спросить модель также о том, в каком состоянии должен находиться автомат в начале работы, чтобы он допустил цепочку аb:
?- допускается( S, [a, b]).
S = s1;
S = s3
Как ни странно, мы можем спросить также "Каковы все цепочки длины 3, допустимые из состояния s1?"
?- допускается( s1, [XI, Х2, X3]).
X1 = а
Х2 = а
Х3 = b;
X1 = b
Х2 = а
Х3 = b;
nо (нет)
Если мы предпочитаем, чтобы допустимые цепочки выдавались в виде списков, тогда наш вопрос следует сформулировать так:
?- Цепочка = [ _, _, _ ], допускается( s1, Цепочка).
Цепочка = [а, а, b];
Цепочка = [b, а, b];
nо (нет)
Можно проделать и еще некоторые эксперименты, например спросить: "Из какого состояния автомат допустит цепочку длиной 7?"
Эксперименты могут включать в себя переделки структуры автомата, вносящие изменения в отношения конечное, переход и спонтанный. В автомате, изображенном на рис. 4.3, отсутствуют циклические "спонтанные пути" (пути, состоящие только из спонтанных переходов). Если на рис. 4.3 добавить новый переход
спонтанный( s1, s3)
то получится "спонтанный цикл". Теперь наша модель может столкнуться с неприятностями. Например, вопрос
?- допускается( s1, [а]).
приведет к тому, что модель будет бесконечно переходить в состояние s1, все время надеясь отыскать какой-либо путь в конечное состояние.
4. 4. Почему не могло возникнуть зацикливание модели исходного автомата на рис. 4.3, когда в его графе переходов не было "спонтанного цикла"?
4. 5. Зацикливание при вычислении допускается можно предотвратить, например, таким способом: подсчитывать число переходов, сделанных к настоящему моменту. При этом модель должна будет искать пути только некоторой ограниченной длины. Модифицируйте так отношение допускается. Указание: добавьте третий аргумент - максимально допустимое число переходов:
допускается( Состояние, Цепочка, Макс_переходов)
Назад | Содержание | Вперёд