Назад | Содержание | Вперёд
В математике мы привыкли записывать выражения в таком виде:
2*a + b*с
где + и * - это операторы, а 2, а, b, с - аргументы. В частности, + и * называют инфиксными операторами, поскольку они появляются между своими аргументами. Такие выражения могут быть
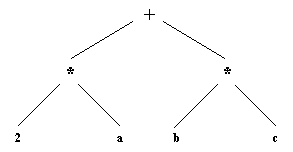
представлены в виде деревьев, как это сделано на рис. 3.6, и записаны как прологовские термы с + и * в качестве функторов:+( *( 2, а), *( b, с) )

Рис. 3. 6. Представление выражения 2*а+b*с в виде дерева.
Поскольку мы обычно предпочитаем записывать такие выражения в привычной инфиксной форме операторов, Пролог обеспечивает такое удобство. Поэтому наше выражение, записанное просто как
2*а + b*с
будет воспринято правильно. Однако это лишь внешнее представление объекта, которое будет автоматически преобразовано в обычную форму прологовских термов. Такой терм выводится пользователю снова в своей внешней инфиксной форме.
Выражения рассматриваются Прологом просто как дополнительный способ записи, при котором не вводятся какие-либо новые принципы структуризации объектов данных. Если мы напишем а + b, Пролог поймет эту запись, как если бы написали +(а, b). Для того, чтобы Пролог правильно воспринимал выражения типа а + b*с, он должен знать, что * связывает сильнее, чем +. Будем говорить, что + имеет более низкий приоритет, чем *. Поэтому верная интерпретация выражений зависит от приоритетов операторов. Например, выражение а + b*с, в принципе можно понимать и как
+( а, *( b, с) )
и как
*( +( а, b), с
)Общее правило состоит в том, что оператор с самым низким приоритетом расценивается как главный функтор терма. Если мы хотим, чтобы выражения, содержащие + и *, понимались в соответствии с обычными соглашениями, то + должен иметь более низкий приоритет, чем *. Тогда выражение а + b*с означает то же, что и а + (b*с). Если имеется в виду другая интерпретация, то это надо указать явно с помощью скобок, например ( а+b)*с.
Программист может вводить свои собственные операторы. Так, например, можно определить атомы имеет и поддерживает в качестве инфиксных операторов, а затем записывать в программе факты вида:
питер имеет
информацию.
пол поддерживает стол.
Эти факты в точности эквивалентны следующим:
имеет( питер,
информацию).
поддерживает( пол, стол).
Программист определяет новые операторы, вводя в программу особый вид предложений, которые иногда называют директивами. Такие предложения играют роль определений новых операторов. Определение оператора должно появиться в программе раньше, чем любое выражение, использующее этот оператор. Например, оператор имеет можно определить директивой
:- ор( 600, xfx, имеет).
Такая запись сообщит Прологу, что мы хотим использовать "имеет" в качестве оператора с приоритетом 600 и типом 'xfx', обозначающий одну из разновидностей инфиксного оператора. Форма спецификатора 'xfx' указывает на то, что оператор, обозначенный через 'f', располагается между аргументами, обозначенными через 'х'.
Обратите внимание на то, что определения операторов не содержат описания каких-либо операций или действий. В соответствии с принципами языка ни с одним оператором не связывается каких-либо операций над данными (за исключением особых, редких случаев). Операторы обычно используются так же, как и функторы, только для объединения объектов в структуры и не вызывают действия над данными, хотя само слово "оператор", казалось бы, должно подразумевать какое-то действие.
Имена операторов это атомы, а их приоритеты - точнее, номера их приоритетов - должны находиться в некотором диапазоне, зависящем от реализации. Мы будем считать, что этот диапазон располагается в пределах от 1 до 1200.(Чем выше приоритет, тем меньше его номер. - Прим. перев
.)Существуют три группы типов операторов, обозначаемые спецификаторами, похожими на xfx:
(1) инфиксные операторы трех типов:
xfx xfy yfx
(2) префиксные операторы двух типов:
fx fy
(3) постфиксные операторы двух типов:
хf yf
Спецификаторы выбраны с таким расчетом, чтобы нагляднее отразить структуру выражения, в котором 'f' соответствует оператору, а 'х' и 'у' представляют его аргументы. Расположение 'f' между аргументами указывает на то, что оператор инфиксный. Префиксные и постфиксные спецификаторы содержат только один аргумент, который, соответственно, либо следует за оператором, либо предшествует ему.
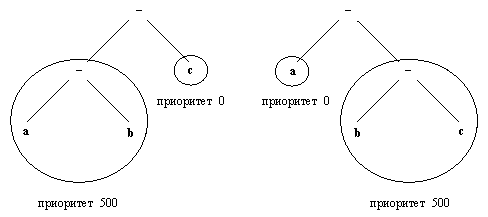
Рис. 3. 7. Две интерпретации выражения а-b-с в предположении, что '-' имеет приоритет 500. Если тип '-' есть yfx, то интерпретация 2 неверна, так как приоритет b-с не выше, чем приоритет '-'.
Между 'х' и 'у' есть разница. Для ее объяснения нам потребуется ввести понятие приоритета аргумента. Если аргумент заключен в скобки или не имеет структуры (является простым объектом), тогда его приоритет равен 0; если же он структурный, тогда его приоритет равен приоритету его главного функтора. С помощью 'х' обозначается аргумент, чей приоритет должен быть строго выше приоритета оператора (т. е. его номер строго меньше номера приоритета оператора); с помощью 'у' обозначается аргумент, чей приоритет выше или равен приоритету оператора.
Такие правила помогают избежать неоднозначности при обработке выражений, в которых встречаются операторы с одинаковым приоритетом. Например, выражение
а-b-с
обычно понимается как (а-b)-с , а не как а-(b-с). Чтобы обеспечить такую обычную интерпретацию, оператор '-' следует определять как yfx. На рис. 3.7 показано, каким образом исключается вторая интерпретация.
В качестве еще одного примера рассмотрим оператор not (логическое отрицание "не"). Если not oпределён как fy, тогда выражение
not not р
записано верно; однако, если not определен как fx, оно некорректно, потому что аргументом первого not является структура not p, которая имеет тот же приоритет, что и not. В этом случае выражение следует писать со скобками:
not (not р)
:- ор( 1200, xfx, ':-').
:- ор( 1200, fx, [:-, ?-] ).
:- op( 1100, xfy, ';').
:- ор( 1000, xfy, ',').
:- op( 700, xfx, [=, is, <<,>, >, =<, >=, ==, =\=, \==, =:=]).
:- op( 500, yfx, [+, -] ).
:- op( 500, fx, [+, -, not] ).
:- op( 400, yfx, [*, /, div] ).
:- op( 300, xfx, mod).
Рис. 3. 8. Множество предопределенных операторов
.Для удобства некоторые операторы в пролог-системах определены заранее, чтобы ими можно было пользоваться сразу, без какого-либо определения их в программе. Набор таких операторов и их приоритеты зависят от реализации. Мы будем предполагать, что множество этих "стандартных" операторов ведет себя так, как если бы оно было определено с помощью предложений, приведенных на рис. 3.8. Как видно из того же рисунка, несколько операторов могут быть определены в одном предложении, если только они все имеют одинаковый приоритет и тип. В этом случае имена операторов записываются в виде списка. Использование операторов может значительно повысить наглядность, "читабельность" программы. Для примера предположим, что мы пишем программу для обработки булевских выражений. В такой программе мы, возможно, захотим записать утверждение одной из теорем де Моргана, которое в математических обозначениях записывается так:
~ (А & В) <===> ~А v ~В
Приведем один из способов записи этого утверждения в виде прологовского предложения:
эквивалентно( not( и( А, В)), или( not( A, not( B))).
Однако хорошим стилем программирования было бы попытаться сохранить по возможности больше сходства между видом записи исходной задачи и видом, используемом в программе ее решения. В нашем примере этого можно достичь почти в полной мере, применив операторы. Подходящее множество операторов для наших целей можно определить так:
:- ор( 800, xfx, <===>).
:- ор( 700, xfy, v).
:- ор( 600, хfу, &).
:- ор( 500, fy, ~).
Теперь правило де Моргана можно записать в виде следующего факта:
~(А & В) <===> ~А v ~В.
В соответствии с нашими определениями операторов этот терм понимается так, как это показано на рис. 3.9.
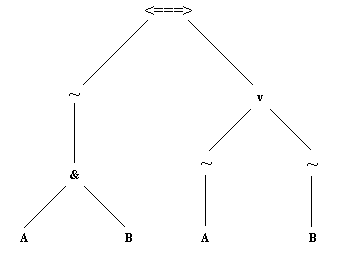
Рис. 3. 9. Интерпретация терма ~(А & В) <===> ~A v ~В
Подытожим:
3. 12. Если принять такие определения
:- ор( 300, xfy, играет_в).
:- ор( 200, xfy, и).
то два следующих терма представляют собой синтаксически правильные объекты:
Tepмl = джимми
играет_в футбол и сквош
Терм1 = сьюзан играет_в
теннис и баскетбол и волейбол
Как эти термы интерпретируются пролог-системой? Каковы их главные функторы и какова их структура?
3. 13. Предложите подходящее определение операторов ("работает", "в", "нашем"), чтобы можно было писать предложения типа:
диана работает секретарем в нашем отделе.
а затем спрашивать:
?- Кто работает
секретарем в нашем отделе.
Кто = диана
?- диана работает
Кем.
Кем = секретарем в нашем
отдела
3. 14. Рассмотрим программу:
t( 0+1, 1+0).
t( X+0+1, X+1+0).
t( X+1+1, Z) :-
t( X+1, X1),
t( X1+1, Z).
Как данная программа будет отвечать на ниже перечисленные вопросы, если '+' "- это (как обычно) инфиксный оператор типа yfx?
(a) ?- t( 0+1, А).
(b) ?- t( 0+1+1, В).
(с) ?- t( 1+0+1+1+1, С).
(d) ?- t( D, 1+1+1+0).
3. 15. В предыдущем разделе отношения между списка ми мы записывали так:
принадлежит(
Элемент, Список),
конк( Список1, Список2,
Список3),
удалить( Элемент, Список,
НовыйСписок), . . .
Предположим, что более предпочтительной для нас является следующая форма записи:
Элемент входит_в
Список,
конкатенация_списков
Список1 и Список2
дает
Список3,
удаление_элемента
Элемент из_списка Список
дает
НовыйСписок, ...
Определите операторы "входит_в", "конкатенация_списков", "и" и т.д. таким образом, чтобы обеспечить эту возможность. Переопределите также и соответствующие процедуры.
Назад | Содержание | Вперёд