Назад | Содержание | Вперёд
В данной главе дается систематическое изложение синтаксиса и семантики основных понятий Пролога, а также вводятся структурные объекты данных. Рассматриваются следующие темы:
Большая часть этих тем уже была затронута в гл. 1. Теперь их изложение будет более формальным и детализированным.
На рис. 2.1 приведена классификация объектов данных Пролога. Пролог-система распознает тип объекта по его синтаксической форме в тексте программы. Это возможно благодаря тому, что синтаксис Пролога

Рис. 2. 1. Обьекты данных Пролога.
предписывает различные формы записи для различных типов объектов данных. В гл. 1 мы уже видели способ, с помощью которого можно отличить атомы от переменных: переменные начинаются с прописной буквы, тогда как атомы - со строчной. Для того, чтобы пролог-система распознала тип объекта, ей не требуется сообщать больше никакой дополнительной информации (такой, например, как объявление типа данных).
В гл. 1 мы уже видели несколько простых примеров атомов и переменных. Вообще же они могут принимать более сложные формы, а именно представлять собой цепочки следующих символов:
Атомы можно создавать тремя способами:
(1) из цепочки букв, цифр и символа подчеркивания _, начиная такую цепочку со строчной буквы:
анна
nil
х25
х_25
х_25AB
х_
х__у
альфа_бета_процедура
мисс_Джонс
сара_джонс
(2) из специальных символов:
<--->
======>
...
.
...
: : =
Пользуясь атомами такой формы, следует соблюдать некоторую осторожность, поскольку часть цепочек специальных символов имеют в Прологе заранее определенный смысл. Примером может служить :- .
(3) из цепочки символов, заключенной в одинарные кавычки. Это удобно, если мы хотим, например, иметь атом, начинающийся с прописной буквы. Заключая его в кавычки, мы делаем его отличным от переменной:
'Том'
' Южная_Америка'
'Сара Джонс'
Числа в Прологе бывают целыми и вещественными. Синтаксис целых чисел прост, как это видно из следующих примеров: 1, 1313, 0, -97. Не все целые числа могут быть представлены в машине, поэтому диапазон целых чисел ограничен интервалом между некоторыми минимальным и максимальным числами, определяемыми конкретной реализацией Пролога. Обычно реализация допускает диапазон хотя бы от -16 383 до 16 383, а часто, и значительно более широкий.
Синтаксис вещественных чисел зависит от реализации. Мы будем придерживаться простых правил, видных из следующих примеров: 3.14, -0.0035, 100.2. При обычном программировании на Прологе вещественные числа используются редко. Причина этого кроется в том, что Пролог - это язык, предназначенный в первую очередь для обработки символьной, а не числовой информации, в противоположность языкам типа Фортрана, ориентированным на числовую обработку. При символьной обработке часто используются целые числа, например, для подсчета количества элементов списка; нужда же в вещественных числах невелика.
Кроме отсутствия необходимости в использовании вещественных чисел в обычных применениях Пролога, существует и другая причина избегать их. Мы всегда стремимся поддерживать наши программы в таком виде, чтобы их смысл был предельно ясен. Введение вещественных чисел в некоторой степени нарушает эту ясность из-за ошибок вычислений, связанных с округлением во время выполнения арифметических действий. Например, результатом вычисления выражения 10000 + 0.0001 - 10000 может оказаться 0 вместо правильного значения 0.0001.
Переменные - это цепочки, состоящие из букв, цифр и символов подчеркивания. Они начинаются с прописной буквы или с символа подчеркивания:
Х
Результат
Объект2
Список_участников
СписокПокупок
_х23
_23
Если переменная встречается в предложения только один раз, то нет необходимости изобретать ей имя. Можно использовать так называемую "анонимную" переменную, которая записывается в виде одного символа подчеркивания. Рассмотрим, например, следующее правило:
Это правило гласит: "Для всех X, Х имеет ребенка, если X является родителем некоторого Y". Здесь мы определяем свойство имеетребенка таким образом, что оно не зависит от имени ребенка. Следовательно, это как раз тот случай, когда уместно использовать анонимную переменную. Поэтому вышеприведенное правило можно переписать так:
Всякий раз, когда в предложения появляется одиночный символ подчеркивания, он обозначает новую анонимную переменную. Например, можно сказать, что существует некто, кто имеет ребенка, если существуют два объекта, такие, что один из них является родителем другого:
Это предложение эквивалентно следующему:
Однако оно имеет совершенно другой смысл, нежели
некто_имеет_ребенка :- родитель( X, X).
Если анонимная переменная встречается в вопросе, то ее значение не выводится при ответе системы на этот вопрос. Если нас интересуют люди, имеющие детей, но не имена этих детей, мы можем просто спросить:
Лексический диапазон имени - одно предложение. Это значит, что если, например, имя Х15 встречается в двух предложениях, то оно обозначает две разные переменные. Однако внутри одного предложения каждое его появлений обозначает одну и ту же переменную. Для констант ситуация другая: один и тот же атом обозначает один и тот же объект в любом предложении, иначе говоря, - во всей программе.
Структурные объекты (или просто структуры) - это объекты, которые состоят из нескольких компонент. Эти компоненты, в свою очередь, могут быть структурами. Например, дату можно рассматривать как структуру, состоящую из трех компонент: день, месяц, год. Хотя они и составлены из нескольких компонент, структуры в программе ведут себя как единые объекты. Для того, чтобы объединить компоненты в структуру, требуется выбрать функтор. Для нашего примера подойдет функтор дата. Тогда дату 1-е мая 1983 г. можно записать так:
дата( 1, май, 1983)
(см. рис. 2.2).
Все компоненты в данном примере являются константами (две компоненты - целые числа и одна - атом). Компоненты могут быть также переменными или структурами. Произвольный день в мае можно представить структурой:
дата( День, май, 1983)
Заметим, что День является переменной и ей можно приписать произвольное значение на некотором более позднем этапе вычислений.
Такой метод структурирования данных прост и эффективен. Это является одной из причин того, почему Пролог естественно использовать для решения задач обработки символьной информации.
Синтаксически все объекты данных в Прологе представляют собой термы. Например,
май
и
суть термы.
Все структурные объекты можно изображать в виде деревьев (пример см. на рис. 2.2). Корнем дерева служит функтор, ветвями, выходящими из него, - компоненты. Если некоторая компонента тоже является структурой, тогда ей соответствует поддерево в дереве, изображающем весь структурный объект.
Наш следующий пример показывает, как можно использовать структуры для представления геометрических объектов (см. рис. 2.3). Точка в двумерном пространстве определяется двумя координатами; отрезок определяется двумя точками, а треугольник можно задать тремя точками. Введем следующие функторы:
точка
для точек
отрезок
для отрезков и
треугольник
для треугольников.
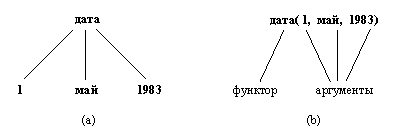
Рис. 2. 2. Дата - пример
структурного объекта:
(а) его представление в виде дерева;
(б) запись на Прологе.
Тогда объекты, приведенные на рис. 2.3, можно представить следующими прологовскими термами:
Р1 = точка( 1, 1)
P2 = точка( 2, 3)
S =
отрезок( P1, P2) =
отрезок( точка( 1, 1), точка( 2, 3) )
Т =
треугольник( точка( 4, 2), точка( 6, 4),
точка( 7, 1) )
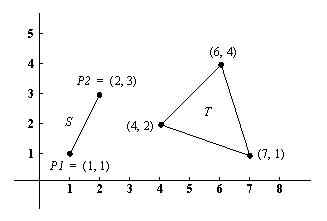
Рис. 2. 3. Простые геометрические объекты.
Соответствующее представление этих объектов в виде деревьев приводится на рис. 2.4. Функтор, служащий
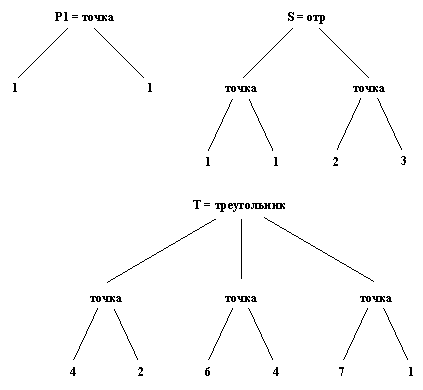
Рис. 2. 4. Представление объектов с рис. 2.3 в виде деревьев.
корнем дерева, называется главным функтором терма.
Если бы в такой же программе фигурировали точки трехмерного пространства, то можно было бы для их представления использовать другой функтор, скажем точка3:
точка3( X, Y, Z)
Можно, однако, воспользоваться одним и тем же именем точка одновременно и для точек двумерного и трехмерного пространств и написать, например, так:
точка( XI, Y1) и точка ( X, Y, Z)
Если одно и то же имя появляется в программе в двух различных смыслах, как в вышеупомянутом примере с точкой, то пролог-система будет различать их по числу аргументов и интерпретировать это имя как два функтора: один - двухаргументный; второй - трех. Это возможно потому, что каждый функтор определяется двумя параметрами:
(1) именем, синтаксис которого совпадает с синтаксисом атомов;
(2) арностью - т. е. числом аргументов.
Как уже объяснялось, все структурные объекты в Прологе - это деревья, представленные в программе термами. Рассмотрим еще два примера, чтобы показать, насколько удобно сложные объекты данных представляются с помощью прологовских термов. На рис. 2.5 показана древовидная структура, соответствующая арифметическому выражению
(а + в)*(с - 5)
В соответствии с введенным к настоящему моменту синтаксисом, такое выражение, используя символы *, + и - в качестве функторов, можно записать следующим образом:
*( +( а, в), -( с, 5) )
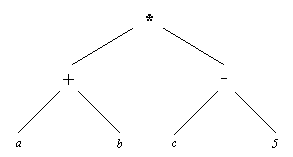
Рис. 2. 5. Древовидная
структура, соответствующая арифметическому
выражению (а + w)*(s - 5).
Это, конечно, совершенно правильный прологовский терм, однако это не та форма, которую нам хотелось бы иметь, при записи арифметических выражений. Хотелось бы применять обычную инфиксную запись, принятую в математике. На самом деле Пролог допускает использование инфиксной нотации, при которой символы *, + и - записываются как инфиксные операторы. Детали того, как программист может определять свои собственные операторы, мы приведем в гл. 3.
В качестве последнего примера рассмотрим некоторые простые электрические цепи, изображенные на рис. 2.6. В правой части рисунка помещены древовидные представления этих цепей. Атомы r1, r2, r3 и r4 - имена резисторов. Функторы пар и посл обозначают соответственно параллельное и последовательное соединение резисторов. Вот соответствующие прологовские термы:
посл( r1, r2)
пар( r1, r2)
паp( rl, пap( r2, r3) )
пар( r1, посл( пар( r2, r3), r4) )
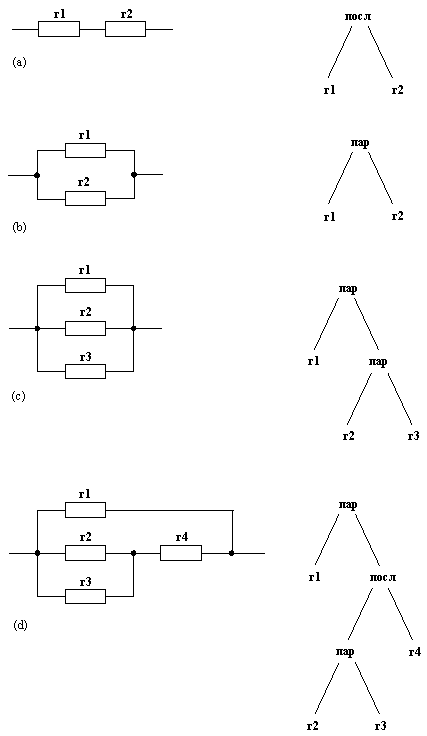
Рис. 2. 6. Некоторые простые электрические цепи и их представление: (а) последовательное соединение резисторов rl и r2; (b) параллельное соединение двух резисторов; (с) параллельное соединение трех резисторов; (d) параллельное соединение r1 и еще одной цепи.
2. 1. Какие из следующих выражений представляют собой правильные объекты в смысле Пролога? Что это за объекты (атомы, числа, переменные, структуры)?
(а) Диана
(b) диана
(с) 'Диана'
(d) _диана
(e) 'Диана
едет на юг'
(f) едет(
диана, юг)
(g) 45
(h) 5( X, Y)
(i) +( север,
запад)
(j) три(
Черные( Кошки) )
2. 2. Предложите представление для прямоугольников, квадратов и окружностей в виде структурных объектов Пролога. Используйте подход, аналогичный приведенному на рис. 2.4. Например, прямоугольник можно представить четырьмя точками (а может быть, только тремя точками). Напишите несколько термов конкретных объектов такого типа с использованием предложенного вами представления.
Назад | Содержание | Вперёд