Назад | Содержание | Вперёд
Для игр, представляющих интерес, полный просмотр игрового дерева невозможен, поэтому были разработаны другие методы, предусматривающие просмотр только части дерева игры. Среди этих методов существует страндартный метод поиска, используемый в игровых (особенно в шахматных) программах и основанный на минимаксном принципе. Дерево игры просматривается только вплоть до некоторой глубины (обычно на несколько ходов), а затем для всех концевых вершин дерева поиска вычисляются оценки при помощи некоторой оценочной функции. Идея состоит в том, чтобы, получив оценки этих терминальных поисковых вершин, не продвигаться дальше и получить тем самым экономию времени. Далее, оценки терминальных позиций распространяются вверх по дереву поиска в соответствии с минимаксным принципом. В результате все вершины дерева поиска получают свои оценки. И наконец, игровая программа, участвующая в некоторой реальной игре, делает свой ход - ход, ведущий из исходной (корневой) позиции в наиболее перспективного (с точки зрения оценки) ее преемника.
Обратите внимание на то, что мы здесь делаем определенное различие между "деревом игры" и "деревом поиска". Дерево поиска - это только часть дерева игры (его верхняя часть), т. е. та его часть, которая была явным образом порождена в процессе поиска. Таким образом, терминальные поисковые позиции совсем не обязательно должны совпадать с терминальными позициями самой игры.
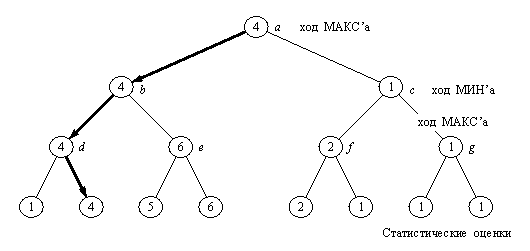
Очень многое зависит от оценочной функции, которая для большинства игр, представляющих интерес, является приближенной эвристической оценкой шансов на выигрыш одного из участников игры. Чем выше оценка, тем больше у него шансов выиграть и чем ниже оценка, тем больше шансов на выигрыш у его противника. Поскольку один из участников игры всегда стремится к высоким оценкам, а другой - к низким, мы дадим им имена МАКС и МИН соответственно. МАКС всегда выбирает ход с максимальной оценкой; в противоположность ему МИН всегда выбирает ход с минимальной оценкой. Пользуясь этим принципом (минимаксным принципом) и зная значения оценок для всех вершин "подножья" дерева поиска, можно определить оценки всех остальных вершин дерева. На рис. 15.2 показано, как это делается. На этом рисунке видно, что уровни позиций с ходом МАКС'а чередуются с уровнями позиций с ходом МИН'а. Оценки вершин нижнего уровня определяются при помощи оценочной функции. Оценки всех внутренних вершин можно определить, двигаясь снизу вверх от уровня к уровню, пока мы не достигнем корневой вершины. В результате, как видно из рис. 15.2, оценка корня оказывается равной 4, и, соответственно, лучшим ходом МАКС'а из позиции а - a-b
. Лучший ответ МИН'а на этот ход - b-d, и т.д. Эту последовательность ходов называют также основным вариантом. Основной вариант показывает, какова "минимаксно-оптимальная" игра для обоих участников. Обратите внимание на то, что оценки всех позиций, входящих в основной вариант, совпадают.
Рис. 15. 2. Статические
(нижний уровень) и минимаксные рабочие
оценки вершин дерева поиска. Выделенные ходы
образуют основной
вариант, т. е. минимаксно-оптимальную игру с
обеих сторон.
Мы различаем два вида оценок: оценки вершин нижнего уровня
и оценки внутренних вершин (рабочие оценки). Первые из них называются также "статическими", так как они вычисляются при помощи "статической" оценочной функции, в противоположность рабочим оценкам, получаемым "динамически" при распространении статических оценок вверх по дереву.Правила распространения оценок можно сформулировать следующим образом. Будем обозначать статическую оценку позиции Р через v( P), а ее рабочую оценку - через V( Р). Пусть Р1, ..., Рn - разрешенные преемники позиции Р. Тогда соотношения между статическими и рабочими оценками можно записать так:
V( Р) = v( P)
если Р - терминальная позиция дерева поиска (n=0)
V( Р) = max V( Рi
)
i
если P - позиция с ходом МАКС'а
V( Р) = min V( Рi
)
i
если Р - позиция с ходом МИН'а
% Минимаксная процедура:
минимакс( Поз, ЛучшПоз, Оц)
% Поз - позиция, Оц - ее минимаксная оценка;
% лучший ход из Поз ведет в позицию ЛучшПоз
минимакс( Поз,
ЛучшПоз, Оц) :-
ходы( Поз, СписПоз), !,
% СписПоз - список разрешенных ходов
лучш( СписПоз, ЛучшПоз, Оц);
стат_оц( Поз, Оц).
% Поз не имеет преемников
лучш( [Поз], Поз, Оц) :-
минимакс( Поз, _, Оц), !.
лучш( [Поз1 |
СписПоз], ЛучшПоз, ЛучшОц) :-
минимакс( Поз1, _, Оц1),
лучш( СписПоз, Поз2, Оц2),
выбор( Поз1, Оц1, Поз2, Оц2, ЛучшПоз, ЛучшОц).
выбор( Поз0, Оц0, Поз1,
Оц1, Поз0, Оц0) :-
ход_мина( Поз0), Оц > Оц1, !;
ход_макса( Поз0), Оц < Оц1, !.
выбор( Поз0, Оц0, Поз1, Оц1, Поз1, Оц1).
Рис. 15. 3. Упрощенная реализация минимаксного принципа.
Программа на Прологе, вычисляющая минимаксную рабочую оценку для некоторой заданной позиции, показана на рис. 15.3. Основное отношение этой программы -
минимакс( Поз, ЛучшПоз, Оц)
где Оц - минимаксная оценка позиции Поз, а ЛучшПоз - наилучшая позиция-преемник позиции Поз (лучший ход, позволяющий достигнуть оценки Оц). Отношение
ходы( Поз, СписПоз)
задает разрешенные ходы игры: СписПоз - это список разрешенных позиций-преемников позиции Поз. Предполагается, что цель ходы имеет неуспех, если Поз является терминальной поисковой позицией (листом дерева поиска). Отношение
лучш( СписПоз, ЛучшПоз, ЛучшОц)
выбирает из списка позиций-кандидатов СписПоз "наилучшую" позицию ЛучшПоз. ЛучшОц - оценка позиции ЛучшПоз, а следовательно, и позиции Поз. Под "наилучшей" оценкой мы понимаем либо максимальную, либо минимальную оценку, в зависимости от того, с чьей стороны ожидается ход.
Назад | Содержание | Вперёд