Назад | Содержание | Вперёд
Для задачи отыскания кратчайшего маршрута (рис. 13.1) И / ИЛИ-граф вместе с функцией стоимости можно определить следующим образом:
Стоимость решающего графа равна сумме стоимостей всех его вершин (в нашем случае это просто сумма стоимостей всех терминальных вершин). В задаче рис. 13.1 стартовая вершина - это а-z. На рис.

Рис. 13. 5. Решающее
дерево минимальной стоимости для задачи
поиска маршрута рис. 13.1, сформулированной в
терминах И / ИЛИ-
графа.
13.5 показан решающий граф, имеющий стоимость 9. Это дерево соответствует пути [a, b, d, f, i, z], который можно построить, если пройти по всем листьям решающего дерева слева направо.
Задача о ханойской башне (рис. 13.6) - это еще один классический пример эффективного применения метода разбиения задачи на подзадачи и построения И / ИЛИ-графа. Для простоты мы рассмотрим упрощенную версию этой задачи, когда в ней участвует только три диска:
Имеется три колышка 1, 2 и 3 и три диска а, b и с (а - наименьший из них, а с - наибольший). Первоначально все диски находятся на колышке 1. Задача состоит в том, чтобы переложить все диски на колышек 3. На каждом шагу можно перекладывать только один диск, причем никогда нельзя помещать больший диск на меньший.
Эту задачу можно рассматривать как задачу достижения следующих трех целей:
(1) Диск а
- на колышек 3.
(2) Диск b
- на колышек 3.
(3) Диск с
- на колышек 3.
Беда в том, что эти цели не независимы. Например, можно сразу переложить диск а на колышек 3, и первая цель будет достигнута. Но тогда две другие цели станут недостижимыми (если только мы не отменим первое наше действие). К счастью, существует такой удобный порядок достижения этих целей, из которого можно легко вывести искомое решение.
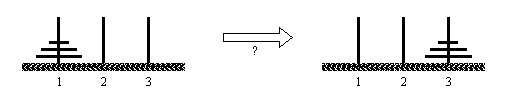
Рис. 13. 6. Задача о ханойской башне
Порядок этот можно установить при помощи следующего рассуждения: самая трудная цель - это цель 3 (диск с - на колышек 3), потому что на диск с наложено больше всего ограничений. В подобных ситуациях часто срабатывает хорошая идея: пытаться достичь первой самую трудную цель. Этот принцип основан на следующей логике: поскольку другие цели достигнуть легче (на них меньше ограничений), можно надеяться на то, что их достижение возможно без отмены действий на достижение самой трудной цели.
Применительно к нашей задаче это означает, что необходимо придерживаться следующей стратегии:
Первой достигнуть цель
"диск с - на колышек 3",
а затем - все остальные.
Но первая цель не может быть достигнута сразу, так как в начальной ситуации диск с двигать нельзя. Следовательно, сначала мы должны подготовить этот ход, и наша стратегия принимает такой вид
(1) Обеспечить
возможность перемещения диска с с 1 на
3.
(2) Переложить
с с 1 на 3.
(3) Достигнуть
остальные цели (а на 3 и b на
3).
Переложить c с 1 на 3 возможно только в том случае, если диск а и b оба надеты на колышек 2. Таким образом наша исходная задача перемещения а, b и с с 1 на 3 сводится к следующим трем подзадачам:
Для того, чтобы переложить a, b и с с 1 на 3, необходимо
(1) переложить
а и b с 1 на 2, и
(2) переложить
с с 1 на 3, и
(1) переложить
а и b с 2 на 3.
Задача 2 тривиальна (она решается за один шаг). Остальные две подзадачи можно решать независимо от задачи 2, так как диски а и b можно двигать, не обращая внимание на положение диска с. Для решения задач 1 и 3 можно применить тот же самый принцип разбиения (на этот раз диск b будет самым "трудным"). В соответствии с этим принципом задача 1 сводится к трем тривиальным подзадачам:
Для того, чтобы переложить а и b с 1 на 2, необходимо:
(1) переложить
а с 1 на 3, и
(2) переложить
b с 1 на 2, и
(1) переложить
а с 3 на 2.
Такие игры, как шахматы или шашки, естественно рассматривать как задачи, представленные И / ИЛИ-графами. Игры такого рода называются играми двух лиц с полной информацией. Будем считать, что существует только два возможных исхода игры: ВЫИГРЫШ и ПРОИГРЫШ. (Об играх с тремя возможными исходами -ВЫИГРЫШ, ПРОИГРЫШ и НИЧЬЯ, можно также говорить, что они имеют только два исхода: ВЫИГРЫШ и НЕВЫИГРЫШ). Так как участники игры ходят по очереди, мы имеем два вида позиций, в зависимости от того, чей ход. Давайте условимся называть участников игры "игрок" и "противник", тогда мы будем иметь следующие два вида позиций: позиция с ходом игрока ("позиция игрока") и позиция с ходом противника ("позиция противника"). Допустим также, что начальная позиция Р - это позиция игрока. Каждый вариант хода игрока в этой позиции приводит к одной из позиций противника Q1, Q2, Q3, ... (см. рис. 13.7). Далее каждый вариант хода противника в позиции Q1 приводит к одной из позиций игрока R11, R12, ... . В И / ИЛИ-дереве, показанном на рис. 13.7, вершины соответствуют позициям, а дуги - возможным ходам. Уровни позиций игрока чередуются в дереве с уровнями позиций противника. Для того, чтобы выиграть в позиции Р, нужно найти ход, переводящий Р в выигранную позицию Qi. (при некотором i). Таким образом, игрок выигрывает в позиции Р, если он выигрывает в Q1, или Q2, или Q3, или ... . Следовательно, Р - это ИЛИ-вершина. Для любого i позиция Qi - это позиция противника, поэтому если в этой позиции выигрывает игрок, то он выигрывает и после каждого вариан-
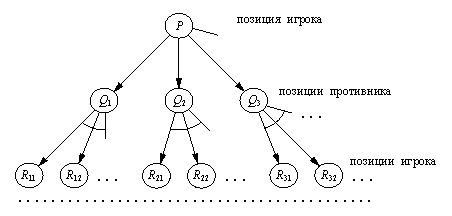
Рис. 13. 7. Формулировка
игровой задачи для игры двух лиц в
форме И / ИЛИ-дерева; участники игры: "игрок"
и "противник".
та хода противника. Другими словами, игрок выигрывает в Qi, если он выигрывает во всех позициях Ri1 и Ri2 и ... . Таким образом, все позиции противника - это И-вершины. Целевые вершины - это позиции, выигранные согласно правилам игры, например позиции, в которых король противника получает мат. Позициям проигранным соответствуют задачи, не имеющие решения. Для того, чтобы решить игровую задачу, мы должны построить решающее дерево, гарантирующее победу игрока независимо от ответов противника. Такое дерево задает полную стратегию достижения выигрыша: для каждого возможного продолжения, выбранного противником, в дереве стратегии есть ответный ход, приводящий к победе.
Назад | Содержание | Вперёд