Назад | Содержание | Вперёд
Рассмотрим следующую задачу планирования. Дана совокупность задач t1, t2, ..., имеющих времена выполнения соответственно T1, Т2, ... . Все эти задачи нужно решить на m идентичных процессорах. Каждая задача может быть решена на любом процессоре, но в каждый данный момент каждый процессор решает только одну из задач. Между задачами существует отношение предшествования, определяющее, какие задачи (если таковые есть) должны быть завершены, прежде чем данная задача может быть запущена. Необходимо распределить задачи между процессорами без нарушения отношения предшествования, причем таким образом, чтобы вся совокупность задач была решена за минимальное время. Время, когда последняя задача в соответствии с выработанным планом завершает свое решение, называется временем окончания плана. Мы хотим минимизировать время окончания по всем возможным планам.
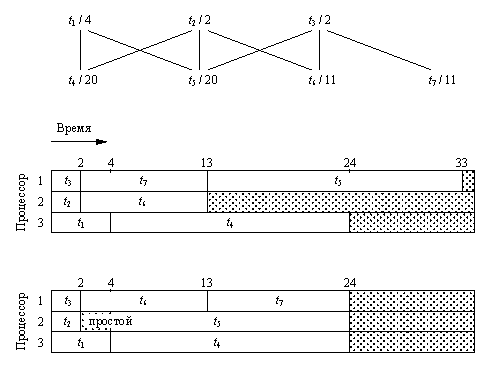
На рис. 12.8 показан пример задачи планирования, а также приведено два корректных плана, один из которых оптимален. Из примера видно, что оптимальный план обладает одним интересным свойством, а именно в нем может предусматриваться "время простоя" процессоров. В оптимальном плане рис. 12.8 процессор 1, выполнив задачу t, ждет в течение двух квантов времени, несмотря на то, что он мог бы начать выполнение задачи t.
Один из способов построить план можно грубо сформулировать так. Начинаем с пустого плана (с незаполненными временными промежутками для каждого процессора) и постепенно включаем в него задачи

Рис. 12. 8. Планирование прохождения задач в многопроцессорной системе для 7 задач и 3 процессоров. Вверху показано предшествование задач и величины продолжительности их решения. Например, задача t5 требует 20 квантов времени, причем ее выполнение может начаться только после того, как будет завершено решение трех других задач t1, t2 и t3. Показано два корректных плана: оптимальный план с временем окончания 24 и субоптимальный - с временем окончания 33. В данной задаче любой оптимальный план должен содержать время простоя.
Coffman/ Denning, Operating Systems Theory, © 1973, p.86. Приведено с разрешения Prentice-Hall, Englewood Cliffs, New Jersey.
одну за другой, пока все задачи не будут исчерпаны. Как правило, на каждом шагу мы будем иметь несколько различных возможностей, поскольку окажется, что одновременно несколько задач-кандидатов ждут своего выполнения. Таким образом, для составления плана потребуется перебор. Мы можем сформулировать задачу планирования в терминах пространства состояний следующим образом:
Этот грубый сценарий требует некоторых уточнений. Во-первых, мы решим заполнять план в порядке возрастания времен, так что задачи будут включаться в него слева направо. Кроме того, при добавлении каждой задачи следует проверять, выполнены ли ограничения, связанные с отношениями предшествования. Далее, не имеет смысла оставлять процессор бездействующим на неопределенное время, если имеются задачи, ждущие своего запуска. Поэтому мы разрешим процессору простаивать только до того момента, когда какой-нибудь другой процессор завершит выполнение своей задачи. В этот момент мы еще раз вернемся к свободному процессору с тем, чтобы рассмотреть возможность приписывания ему какой-нибудь задачи.
Теперь нам необходимо принять решение относительно представления проблемных ситуаций, т.е. частичных планов. Нам понадобится следующая информация:
(1) список ждущих задач вместе с их временами выполнения;
(2) текущая загрузка процессоров задачами.
Добавим также для удобства программирования
(3) время окончания (частичного) плана, т.е. самое последнее время окончания задачи среди всех задач, приписанных процессорам.
Список ждущих задач вместе с временами их выполнения будем представлять в программе при помощи списка вида
[ Задача1/Т1, Задача2/Т2, ... ]
Текущую загрузку процессоров будем представлять как список решаемых задач, т. е. список пар вида
[ Задача/ВремяОкончания ]
В списке m таких пар, по одной на каждый процессор. Новая задача будет добавляться к плану в момент, когда закончится первая задача из этого списка. В связи с этим мы должны постоянно поддерживать упорядоченность списка загрузки по возрастанию времен окончания. Эти три компоненты частичного плана (ждущие задачи, текущая загрузка и время окончания плана) будут объединены в одно выражение вида
Ждущие * Активные * ВремяОкончания
Кроме этой информации у нас есть ограничения, налагаемые отношениями предшествования, которые в программе будут выражены в форме отношения
предш( ЗадачаX, ЗадачаY)
Рассмотрим теперь эвристическую оценку. Мы будем использовать довольно примитивную эвристическую функцию, которая не сможет обеспечить высокую эффективность управления алгоритмом поиска. Эта функция допустима, так что получение оптимального плана будет гарантировано. Однако следует заметить, что для решения более серьезных задач планирования потребуется более мощная эвристика.
Нашей эвристической функцией будет оптимистическая оценка времени окончания частичного плана с учетом всех ждущих задач. Оптимистическая оценка будет вычисляться в предположении, что два из ограничений, налагаемых на действительно корректный план, ослаблены:
(1) не учитываются отношения предшествования;
(2) делается (не реальное) допущение, что возможно распределенное выполнение задачи одновременно на нескольких процессорах, причем сумма времен выполнения задачи на процессорах равна исходному времени выполнения этой задачи на одном процессоре.
Пусть времена выполнения ждущих задач равны Т1, Т2, ..., а времена окончания задач, выполняемых на процессорах - К1, К2, ... . Тогда оптимистическая оценка времени ОбщКон окончания всех активных к настоящему моменту, а также всех ждущих задач имеет вид:
![]()
где m - число процессоров. Пусть время окончания текущего частичного плана равно
Кон = maх(Kj).
j
Тогда эвристическая оценка Н
(дополнительное время для включения в частичный
план ждущих задач) определяется следующим
выражением:
if ОбщКон>Кон then Н = ОбщКон-Кон else H=0
Программа, содержащая определения отношений, связанных с пространством состояний нашей задачи планирования, приведена полностью на рис. 12.9. Эта программа включает в себя также спецификацию конкретной задачи планирования, показанной на рис. 12.3. Одно из оптимальных решений, полученных в процессе поиска с предпочтением в определенном таким образом пространстве состояний, показано на рис. 12.8.
Вообще говоря, задачи планирования характеризуются значительной комбинаторной сложностью. Наша простая эвристическая функция не обеспечивает высокой эффективности управления поиском. Предложите другие эвристические функции и проведите с ними эксперименты.
/* Отношения для задачи планирования.
Вершины пространства состояний - частичные
планы,
записываемые как
[ Задача1/Т1,
Задача2/Т2, ...]*
[ Задача1/К1, Задача2/К2, ...]*
ВремяОкончания
В первом списке указываются ждущие задачи и
продолжительности их выполнения; во втором -
текущие решаемые задачи и их времена окончания,
упорядоченные так, чтобы выполнялись
неравенства K1<=K2, K2<=K3, ... . Время окончания
плана - самое последнее по времени время
окончания задачи.
*/
после( Задачи1*[ _ /К |
Акт1]*Кон1, Задачи2*Акт2*Кон2,Ст):-
удалить( Задача/Т, Задачи1, Задачи2),
% Взять ждущую задачу
not( принадлежит( Здч1/_, Задачи2),
раньше( ЗДЧ, Задача) ),
% Проверить предшествование
not( принадлежит( Здч1/К1, Акт1), К1<К2,
раньше( К1, Задача) ), % Активные
задачи
Время is К + Т,
% Время окончания работающей задачи
встав( ЗадачаВремя, Акт1, Акт2, Кон1, Кон2),
Ст is Кон2 - Кон1.
после( Задачи*[ _ /К |
Акт1]*Кон, Задачи2*Акт2*Кон, 0):-
вставпростой( К, Акт1, Акт2).
% Оставить процессор бездействующим
раньше( Задача1,
Задача2) :-
% В соответствии с предшествованием
предш( Задача1, Задача2).
% Задача1 раньше, чем Задача2
раньше( Здч1, Здч2) :-
предш( Здч, Здч2),
раньше( Здч1, Здч).
встав( Здч/А, [Здч1/В |
Спис], [Здч/А, Здч1/В | Спис], К, К):-
% Список задач упорядочен
А =< В, !.
встав( Здч/А, [Здч1/В |
Спнс], [Здч1/В | Спис1], К1, К2) :-
встав( Здч/А, Спис, Спис1, Kl, К2).
встав( Здч/А, [ ], [Здч/А], _, А).
вставпростой( А,
[Здч/В | Спис], [простой/В, Здч/В | Спис]):-
% Оставить процессор бездействующим
А < В, !
%
До ближайшего времени окончания
вставпростой( А,
[Здч/В | Спис], [Здч/В | Спис1]) :-
вставпростой( А, Спис, Спис1 ).
удалить( А, [А | Спис],
Спис ).
% Удалить элемент из списка
удалить( А, [В | Спис],
[В | Спис1] ):-
удалить( А, Спис, Спис1 ).
цель( [ ] *_*_ ). % Целевое состояние: нет ждущих задач
% Эвристическая оценка частичного плана
основана на
% оптимистической оценке последнего времени
окончания
% этого частичного плана,
% дополненного всеми остальными ждущими
задачами.
h( Задачи *
Процессоры * Кон, Н) :-
сумвремя( Задачи, СумВремя),
% Суммарная продолжительность
% ждущих задач
всепроц( Процессоры, КонВремя, N),
% КонВремя - сумма времен окончания
% для процессоров, N - их количество
ОбщКон is ( СумВремя + КонВремя)/N,
( ОбщКон > Кон, !, H is ОбщКон - Кон; Н = 0).
сумвремя( [ ], 0).
сумвремя( [ _ /Т |
Задачи], Вр) :-
сумвремя( Задачи, Вр1),
Вр is Bp1 + Т.
всепроц( [ ], 0, 0).
всепроц( [ _ /T |
СписПроц], КонВр, N) :-
всепроц( СписПроц, КонВр1, N1),
N is N1 + 1,
КонВр is КонВр1 + Т.
% Граф предшествования задач
предш( t1, t4). предш( t1, t5). предш( t2, t4).
предш( t2, t5). предш( t3, t5). предш( t3, t6).
предш( t3, t7).
% Стартовая вершина
старт( [t1/4, t2/2, t3/2,
t4/20, t5/20, t6/11, t7/11] *
[простой/0, простой/0, простой/0] * 0 ).
Рис. 12. 9. Отношения для
задачи планирования. Даны также
определения отношений для конкретной задачи
планирования с
рис. 12.8: граф предшествования и исходный
(пустой) план в
качестве стартовой вершины.
Программа поиска с предпочтением, представленная в настоящей главе, - это один из многих вариантов похожих друг на друга программ, из которых А*-алгоритм наиболее популярен. Общее описание А*-алгоритма можно найти в книгах Nillson (1971, 1980) или Winston (1984). Теорема о допустимости впервые доказана авторами статьи Hart, Nilsson, and Raphael (1968). Превосходное и строгое изложение многих разновидностей алгоритмов поиска с предпочтением и связанных с ними математических результатов дано в книге Pearl (1984). В статье Doran and Michie (1966) впервые изложен поиск с предпочтением, управляемый оценкой расстояния до цели.
Головоломка "игра в восемь" использовалась многими исследователями в области искусственного интеллекта в качестве тестовой задачи при изучении эвристических принципов (см., например, Doran and Michie (1966), Michie and Ross (1970) и Gaschnig (1979) ).
Задача планирования, рассмотренная в настоящей главе, также как и многие ее разновидности, возникает во многих прикладных областях в ситуации, когда необходимо спланировать обслуживание запросов на ресурсы. Один из примеров - операционные системы вычислительных машин. Задача планирования со ссылкой на это конкретное приложение изложена в книге Coffman and Denning (1973).
Найти хорошую эвристику - дело важное и трудное, поэтому изучение эвристик - одна из центральных тем в искусственном интеллекте. Существуют, однако, некоторые границы, за которые невозможно выйти, двигаясь в направлении улучшения качества эвристик. Казалось бы, все, что необходимо для эффективного решения комбинаторной задачи - это найти мощную эвристику. Однако есть задачи (в том числе многие задачи планирования), для которых не существует универсальной эвристики, обеспечивающей во всех случаях как эффективность, так и допустимость. Многие теоретические результаты, имеющие отношение к этому ограничению, собраны в работе Garey and Johnson (1979).
Coffman E.G. and Denning P.J. (1973). Operating Systems Theory. Prentice-Hall.
Doran J. and Michie D. (1966). Experiments with the graph traverser program. Proc. Royal Socieiy of London 294(A): 235-259.
Garey M. R. and Johnson D. S. (1979). Computers and Intractability. W. H. Freeman. [Имеется перевод: Гэри M., Джонсон Д. С- Вычислительные машины и труднорешаемые задачи.- M.: Мир, 1982.]
Gaschnig J. (1979). Performance measurement and analysis of certain search algorithms. Carnegie-Mellon University: Computer Science Department-Technical Report CMU-CS-79-124 (Ph. D. Thesis).
Hart P.E., Nilsson N.J. and Raphael B. (1968). A formal basis for the heuristic determination of minimum cost paths. IEEE Transactions on Systems Sciences and Cybernetics SSC-4(2):100-107
Michie D. and Ross R. (1970). Experiments with the adaptive graph traverser. Machine Intelligence 5: 301-308.
Nilsson N.J. (1971). Problem - Solving Methods in Artificial Intelligence. McGraw-Hill. [Имеется перевод: Нильсон H. Искусственный интеллект. Методы поиска решений. - M: Мир, 1973.]
Nilsson N. J. (1980). Principles of Artificial Intelligence. Tioga; also Springer-Verlag.
Pearl J. (1984). Heuristics: Intelligent Search Strategies for Computer Problem Solving. Addison-Wesley.
Winston P. H. (1984). Artificial Intelligence (second edition). Addison-Wesley. [Имеется перевод первого издания: Уинстон П. Искусственный интеллект. - M.: Мир, 1980.]
Назад | Содержание | Вперёд